Algorithm Analysis: Greedy Algorithm 3
알고리즘 관련 모든 글은 연세대학교 안형찬 교수님의 CSI_3108: Algorithm Analysis의 강의 내용과 자료입니다.
이번 글에서는 greedy algorithm의 또다른 증명 방법인 Exchange argument 방식을 살펴보려 합니다. 그러기에 앞서 새로운 문제를 풀어보겠습니다.
Scheduling to Minimize Lateness

문제 자체는 이번에도 꽤 간단합니다. 비슷하게 어떤 job이 있고 이를 소화 또는 처리하는 기계가 있습니다. 어떻게 스케줄링을 할지의 문제입니다. 다만 앞서 살펴봤던 Interval scheduling 문제와 약간 다른 점이라면, 각 job의 starting time이나 finishing time은 주어져있지 않습니다. 그대신 그 job이 처리하는 데에 소요되는 시간(processing time, $p_i$)과 마감기한(due date, $d_i$)이 있다. 이에 따라 data 1개는 $(p_i, d_i)$ 로 표현됩니다. 각 job의 starting time $s(i)$나 finishing time $f(i)$는 우리 알고리즘에서 정해집니다. 우리가 그 job을 시작하게 되는 시간이 곧 s(i)고 거기에 소요시간을 더한 것이 f(i)가 되는 식입니다.
그리고 여기서 정의하는 가장 주요 개념인 lateness는 그 job이 끝나는 시간 f(i)가 마감기한(due date)를 얼만큼 넘겼는지를 가리킵니다. 여러 job들이 있고, 마감기한을 넘어서 처리되는 애들이 있을텐데, 그 마감을 넘겨서 처리되는 애들 중 가장 늦게 처리되는 애의 lateness가 $L$ 표시됩니다. 이 $L$을 최대한 작게 하도록 하는 것이 알고리즘의 목표인 것입니다. 아래 그림이 간단한 예시를 보여줍니다.
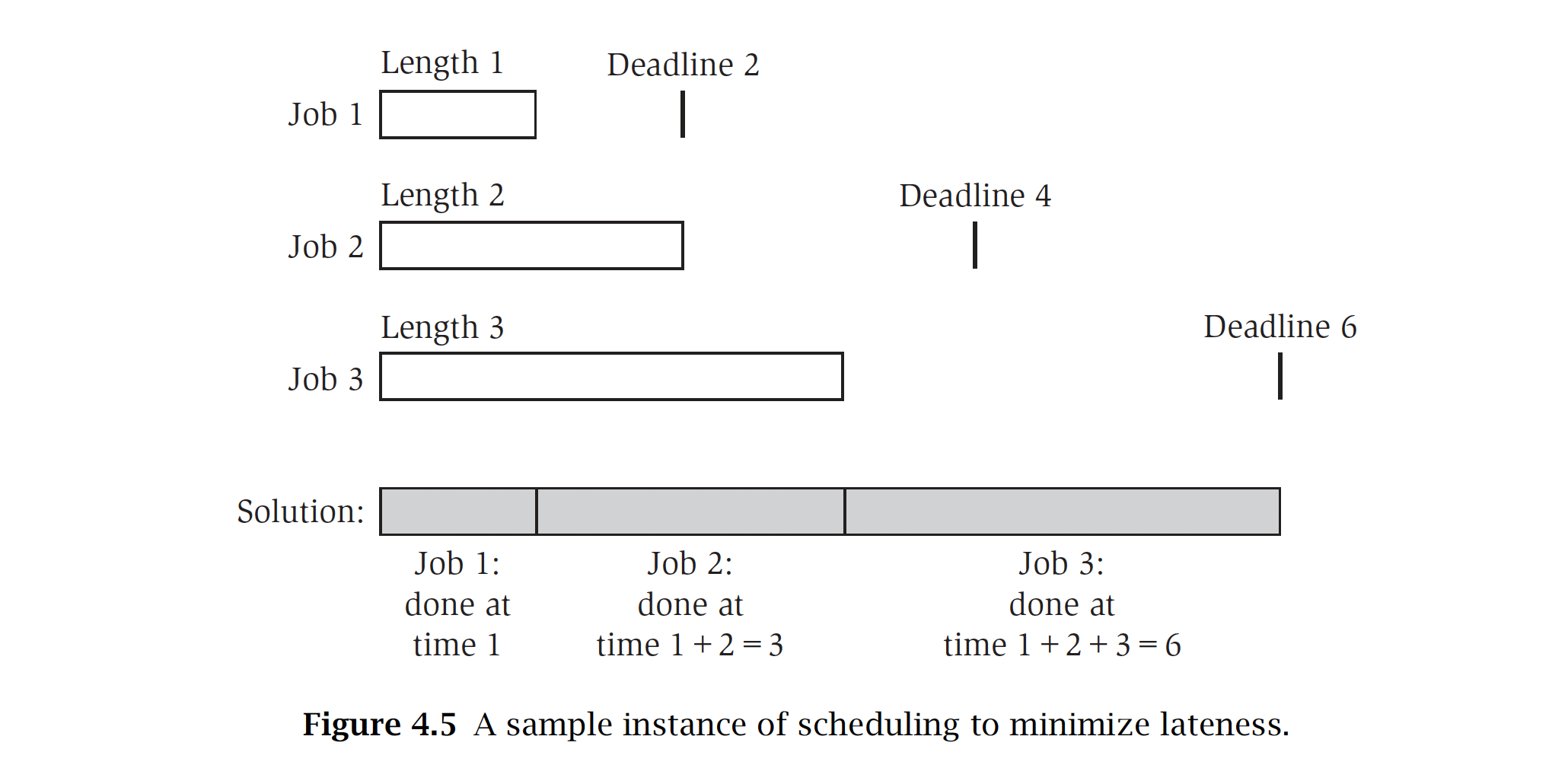
여기서도 여러 가지 방법이 떠오릅니다. 예를 들어 짧은 애들부터 얼른 처리한다든지, 아니면 slack이 가장 작은 애부터 처리한다든지 등등이 있겠습니다. Slack은 마감기한과 소요시간의 차이를 뜻합니다($d_i-p_i$). 후자의 방법은 이런 반례가 존재할 수 있습니다. $p_1=1$, $d_1=2$, $p_2=10$, $d_2=10$. 그러면 job2의 slack은 0이 되어 job2를 가장 먼저 처리하게 되고, job1은 심하게 늦어져버립니다.
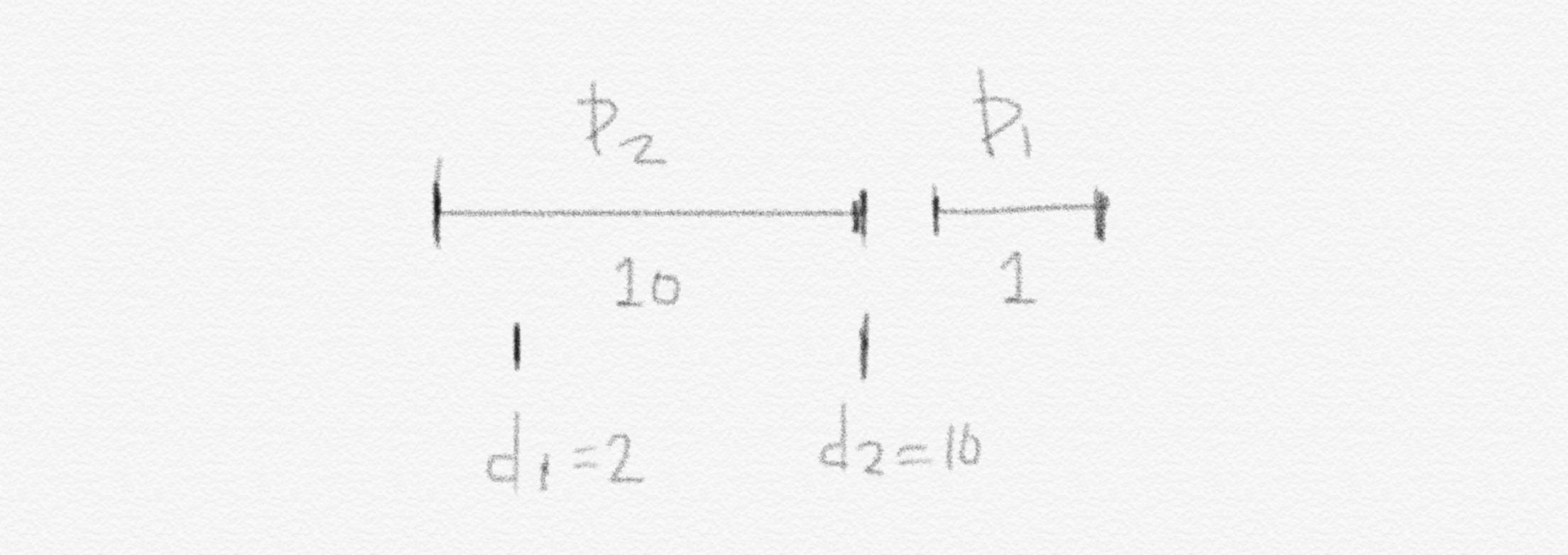
이 문제를 해결하는 algorithm을 사실 우리는 이미 매일 실천하고 있습니다. 바로 마감이 가장 코앞인 것부터 해치우는 방식입니다. 이를 좀 멋진 표현으로 EDD rule (Earliest Due Date) 이라고 합니다.
Algorithm
due date가 빠른 순으로 job들을 정렬합니다
f = 0
for each job in 정렬된 list:
s(i) = f
f = f + p_i
알고리즘은 매우 간단합니다. 한 가지 특징이 있다면, 기계가 쉬지 않는다는 것입니다. 모든 job이 끝나기 전까지, 하나의 job이 끝나면 바로 이어서 다른 job을 처리합니다. 이렇게 우리 알고리즘에 의한 스케줄링에서는 기계가 노는 시간(idle time)이 없습니다.
Definition. We say a schedule has idle time $t$, if there exists some time point $0 \le t < t’$ such that the machine has a job scheduled at time $t’$ but not at time $t$.
우리의 문제에서는 maximum lateness만 minimize 하는 스케줄을 짜라고 했지, 노는 시간이 없는 스케줄을 짜라고 한 적은 없습니다. 그런데 우리 알고리즘은 노는 시간이 없는 스케줄만 리턴됩니다. 따라서, optimal solution 중에서 노는 시간이 없는 optimal solution이 존재한다는 사실을 따로 증명해줄 필요가 있습니다.
Lemma 1.
Optimal solution 중에서 노는 시간(idle time)이 없는 solution이 존재한다.
$Proof.$
만약 어떤 optimal solution에 노는 시간이 있다고 가정해보겠습니다. 그러면 그 노는 시간 후에 있는 스케줄들을 앞으로 당겨오는 방식 혹은 idle time을 squeeze 하는 방식을 취하면 maximum lateness를 증가시키지 않으면서 노는 시간을 없앨 수 있습니다.
이 Lemma.1이 있기 때문에 이제 우리는 스케줄을 job들의 순열(permutation)로 취급할 수 있습니다. 그리고 EDD rule은 job들을 sorting하는 것으로 해석될 수 있습니다. 이를 증명하는 과정은 약간 bubble sort와 유사합니다.
Lemma 2.
Optimal solution 중에서 inversion이 없는 solution이 존재한다.
(Inversion 이란, due date 빠른 순으로 정렬되어 있는 와중에, due date 느린 job 하나가 due date 빠른 job보다 앞에 먼저 배치되는 상황을 의미합니다.)
$Proof.$
만약 어느 하나의 optimal solution $O$에 inversion이 존재한다고 가정해보겠습니다. 이 inversion은 바로 앞뒤로 붙어있는 job 2개의 경우에만 생깁니다. 만약 연달아 있는 job이 아닌 서로 떨어져서 존재한다면 그 두 job 사이에 있는 애들은 제대로 정렬되어 있다는 의미인데, 이는 모순입니다.
이제 이 inversion이 있는 두 job를 swap하는 것을 생각해보겠습니다. 우리는 이렇게 $O$를 swap한 이후의 스케줄 $\bar O$의 maximum lateness가 더 증가하지 않았다는 것을 이제 보이고자 합니다. 어느 한 optimal solution $O$의 어느 한 job $a$의 시작 시간, 끝나는 시간, 그리고 lateness를 각각 $s(a), f(a), l(a)$ 로 나타내겠습니다. 그리고 $\bar s(a), \bar f(a),\bar l(a)$ 는 swap 한 이후의 시작 시간, 끝나는 시간, lateness 입니다.
이제 inversion이 있는 두 job $i, j$를 생각해보겠습니다. $f(i)$와 $f(j)$가 아래처럼 있습니다. 이를 이제 swap한 후의 finishing time은 $\bar f(i)$와 $\bar f(j)$ 가 됩니다.
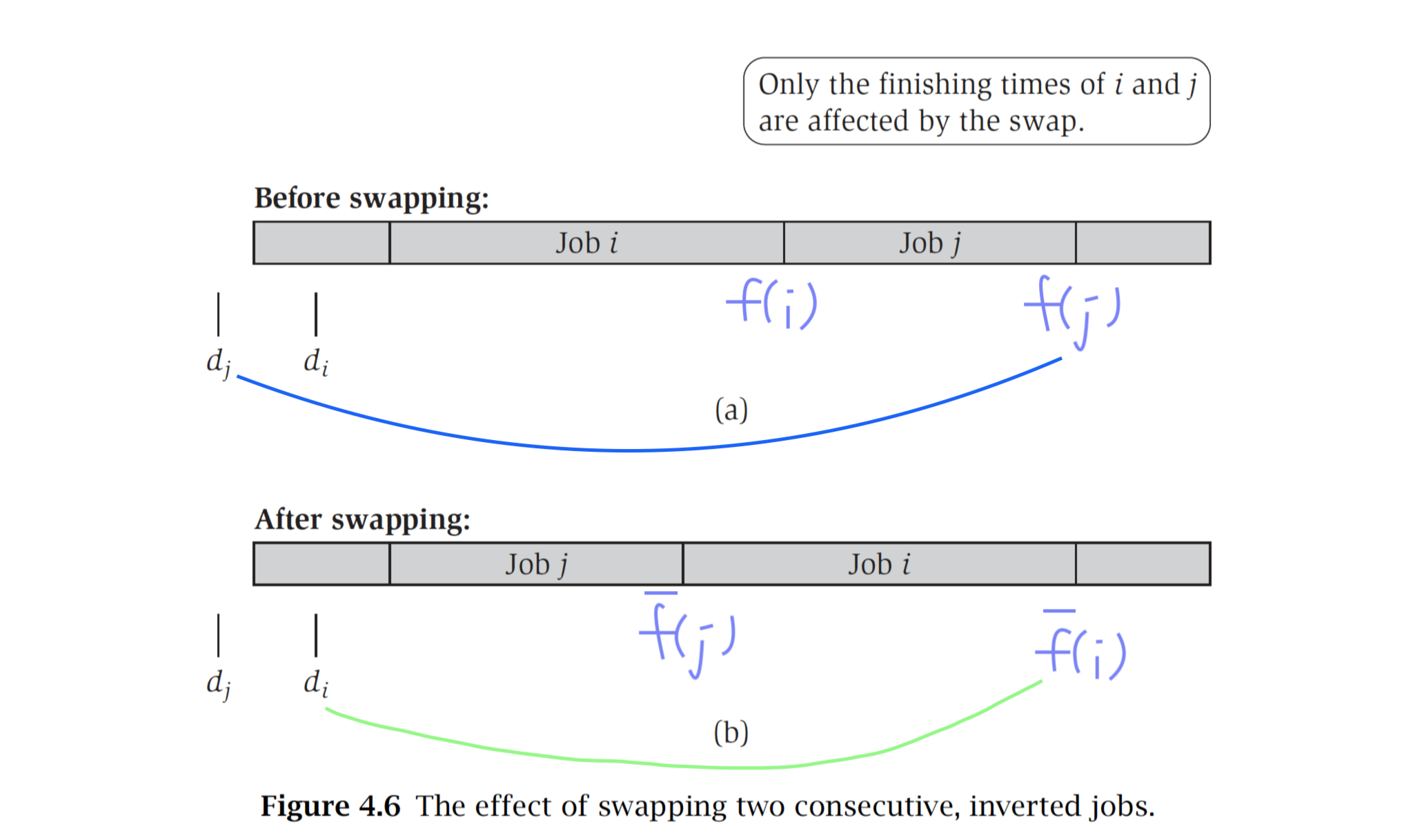
그림에도 나와있는 것처럼 swap이후의 job $i$의 finishing time인 $\bar f(i)$ 는 swap하기 이전에 job $j$ 의 finishing time인 $f(j)$ 과 같아집니다( $\bar f(i) = f(j)$ ). 그렇기 때문에 inversion이 있을 때나, 없앤 후나 두 job이 끝나는 시간은 동일하므로 다른 job들의 lateness에는 변화가 없습니다. 따라서 우리는 두 job의 lateness만 신경 쓰면 됩니다. 그리고 나아가 우리가 신경 쓰는 것은 maximum lateness이기 때문에 두 job들 중 더 늦는 것에만 초점을 맞추면 됩니다. Swap되기 전에는 job $j$의 lateness가 job $i$의 lateness보다 크니 job $j$가 관건입니다. Swap 이후에는 job $i$ 의 lateness가 job $j$의 lateness보다 크므로 job $i$만 신경 쓰겠습니다. 그러면 그 둘의 lateness 를 비교해보겠습니다.
그림을 보면 좀더 직관적으로 와닿습니다. Swap을 해도 maximum lateness는 증가하지 않습니다. 따라서 optimal $O$에 inversion이 존재하더라도 이를 swap 해나가면 됩니다.
Lemma 3.
Inversion과 idle time이 없는 스케줄들은 모두 같은 maximum lateness를 갖는다.
$Proof.$
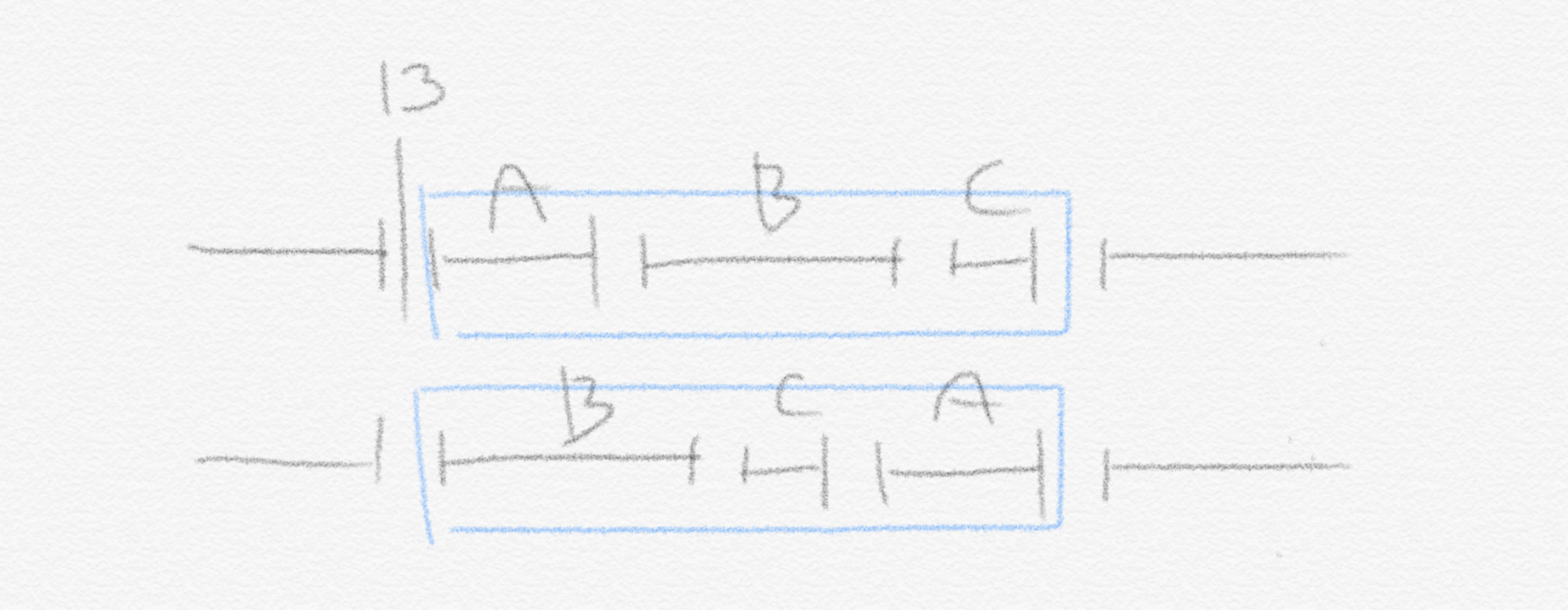
만약 서로 다른 두 스케줄에 inversion과 idle time이 없다고 할 때, 그 두 스케줄은 순서에 있어서 좀 다를 수 있습니다. 하지만 마감기한이 똑같은 job들 사이에서만 순서가 다를 것입니다. 예를 들어, 마감기한이 10일인 job이 있고, 13일인 job이 있고, 14일인 job이 있다고 가정해보겠습니다. 그러면 똑같이 마감 기한이 13일인 여러 job들(A, B, C)은 각 스케줄마다 순서가 좀 다를 수 있습니다. 그러면 이들 중 가장 큰 lateness를 갖는 job은 그 마감기한이 13일인 job들 중 가장 늦게 처리되는 job입니다. 그런데 이들 중 가장 큰 lateness의 값은 job의 순서와 관계 없습니다. 왜냐하면 어차피 그 job들은 모두 마감기한이 13일로 똑같기 때문입니다.
A, B, C의 greatest lateness는 C의 lateness입니다. B, C, A의 greatest lateness는 A의 lateness입니다. 하지만 아래 그림에서 보다시피 그 둘의 lateness는 똑같습니다(13일로부터의 거리가 똑같습니다).
Theorem 1.
The given algorithm is correct.
$Proof.$
우리가 앞서 살펴봤던 Lemma 들을 한 데 엮으면 당연한 말이 됩니다.
- Optimal solution에 idle time이 존재하더라도 maximum lateness를 증가시키지 않으면서 다 없앨 수 있습니다.
- Optimal solution에 inversion이 존재하더라도 maximum lateness를 증가시키지 않으면서 swap을 하면 다 없앨 수 있습니다.
- 따라서 idle time과 inversion이 없는 optimal solution이 존재합니다
- Idle time과 inversion이 없는 모든 스케줄들은 maximum lateness가 같습니다
- 우리의 알고리즘이 리턴하는 스케줄에는 idle time과 inversion이 없습니다.
- 따라서 우리의 알고리즘이 리턴하는 스케줄은 optimal solution과 퀄리티가 같습니다.
Running time
Due date 순으로 정렬해서 문제를 풀면 되므로 자연스럽게 시간복잡도는 $O(nlogn)$ 이 됩니다.
정리
우리 알고리즘이 리턴하는 스케줄의 특성(idle time없음, inversion없음)을 파악하고, optimal solution을 하나 가정합니다. 그리고 이 optimal solution도 목표하는 바(maximum lateness를 최소화)를 악화시키지 않으면서 몇 가지를 바꾸어 나가면서 우리 알고리즘이 리턴하는 스케줄과 같은 형태로 만들 수 있다는 사실을 보입니다. 이렇기 때문에 이 접근방식을 Exchange argument 증명방법이라 합니다.
Greedy algorithm 종합 정리
Greedy algorithm 증명에서는 대개 optimal solution 혹은 여타 solution $O$ 를 가정해놓고 이보다 우리의 결과 $A$ 가 나쁘지 않다는 것을 보이는 방식으로 나아갑니다. 그래야지 우리의 solution $A$ 가 local optimum이 아닌 global optimum임을 보일 수 있습니다. 물론 다른 증명 방법도 있습니다. 애초에 문제의 지형 자체가 optimum이 1개만 존재하는 지형이라는 사실을 보임으로써 local optimum=global optimum임을 보이는 방법이 존재합니다. 하지만 이 방법은 더 엄밀성을 요구하여 난이도가 높습니다.
- Algorithm Analysis - Greedy Algorithm 1 SERIES 1/3
- Algorithm Analysis - Greedy Algorithm 2 SERIES 2/3
- Algorithm Analysis - Greedy Algorithm 3 ✓ SERIES 3/3