Algorithm Analysis: Greedy Algorithm 2
알고리즘 관련 모든 글은 연세대학교 안형찬 교수님의 CSI_3108: Algorithm Analysis의 강의 내용과 자료입니다.
지난 글에 이어서 Interval scheduling 문제를 또다른 증명 방법인 Certificate 방식으로 접근해보겠습니다.
Interval Scheduling
Suppose you are in charge of organizing the schedule of a lecture room. Given a set of room requests, you want to serve as many requests as possible. Each request is in the form of a time interval for which the room is requested, and you cannot serve two requests whose intervals overlap.
Let $n$ be the number of given requests, or intervals. We will represent each interval by a number in $I := {1,…, n}$. Let $s(i)$ and $f(i)$ respectively denote the starting time and finishing time of interval $i \in I$. We assume $s(i) < f(i)$ for all $i$.
Definition 1. We say two intervals $i$ and $j$ are compatible if either $f(i) \le s(j)$ or $f(j) \le s(i)$.
Definition 2. We say a set of intervals is compatible if every pair of intervals in the set is compatible.
We are now ready to formally state the problem.
Problem 1. Given a set of $n$ intervals $1,…,n$, find a maximum-cardinality subset of intervals that is compatible.
각 interval은 시작점 $s(i)$와 끝점 $f(i)$를 갖고 있고, 우리의 목표는 이런 interval들이 겹치지 않게(=compatible) 스케줄을 만들면서, 최대한 많은 interval을 소화하는 것입니다.
Proof by certificates
Interval들의 집합 $I$ 가 주어져있을 때, $OPT(I)$ 는 $I$ 의 compatible subset의 maximum cardinality(원소 개수)를 나타냅니다. 우리가 아래와 같은 Interval scheduling의 어떤 instance $I’$가 주어졌다고 가정해보겠습니다.

Lower bound
만약 우리가 알고리즘이나 자료구조 같은 거는 하나도 알지 못 하는 친구에게 여기서 $OPT(I’) \ge 3$ 임을 보이려면 어떻게 해야 할지 생각해보겠습니다. 적어도 $OPT(I’)$ 가 3 이상은 된다는 사실 말입니다. 이는 생각보다 간단합니다. 친구에게 3개짜리 예시를 아래처럼 보여주면 끝입니다.
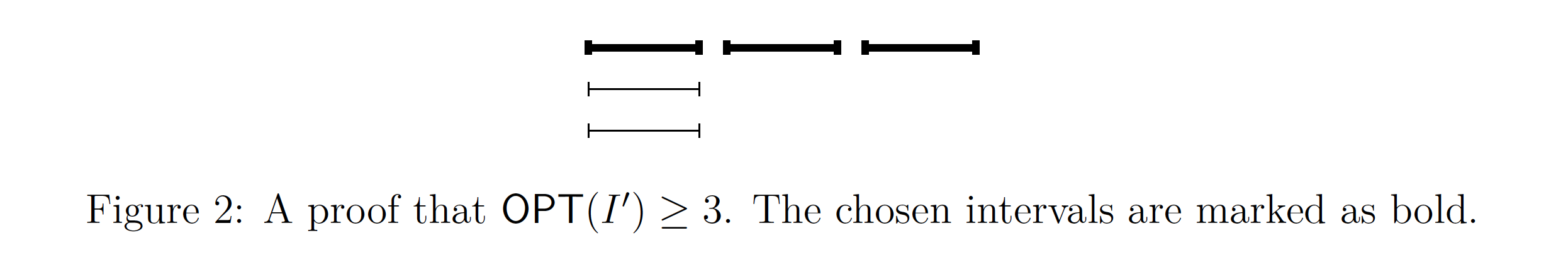
이 3개짜리 예시는 이렇게 3개짜리가 이미 있으니, $OPT(I’)$ 는 못해도 3은 된다는 보증(certificate)이 됩니다. 일반화를 해보면 $OPT(I’) \ge k $ 임을 보이기 위해서는 k개의 interval로 이루어진 compatible한 subset 예시를 보이면 됩니다. 다시 말해 ,이런 예시 하나가 $OPT(I’)$ 의 lower bound의 역할을 합니다. 아래는 이를 엄밀히 표현한 것입니다.
Observation 1. If $J \subseteq I$ is compatible, we have $ OPT(I) \ge |J|$.
Upper bound
이제 lower bound를 잡았으니, $OPT(I’)$ 의 upper bound도 잡아보겠습니다. 지금 우리의 $I’$ 를 보면 $OPT(I’) \le 5$ 라는 사실을 바로 알 수 있습니다. 어떻게 알 수 있냐면, 주어진 interval의 개수가 5개뿐이기 때문입니다. 애초에 주어진 interval이 5개밖에 없는데 $OPT(I’)$ 가 5를 넘을 수는 없는 노릇입니다. 그렇다면 $OPT(I’) \le 3$ 은 어떻게 보일 수 있을까요? 아래 그림을 보겠습니다.

색깔이 같은 애들끼리 하나의 subset을 이룹니다. 그리고 위의 그림에서 서로 똑같은(서로 겹치는) interval들끼리만 하나의 subset을 이루고 있습니다. 따라서 하나의 subset에서 선택될 수 있는 interval은 최대 1개입니다. 그러므로 각 subset마다 최대 1개씩만 선택할 수 있기 때문에 최대 3개의 interval만 가능합니다, $OPT(I’) \le 3$ . 그리고 이 각 subset을 partition이라고 할 수 있습니다. Partition이란, 서로 disjoint하고 그리고 이들을 합하면 전체 set이 나오는 subset들을 지칭합니다. 정리해보겠습니다.
Definition 1. We say $ I_1,…, I_k$ is a partition of $I$ if $I_1,…, I_k$ are mutually distjoint and $\cup^k_{i=1}I_i = I$.
Observation 2. If $ I_1,…, I_k$ is a partition of $I$ such that the intervals in $I_i$ are identical for all $i = 1,…, k$, we have $OPT(I) \le k$ .
하지만 불행히도 이는 좀 뭔가 허술한 면이 있습니다. 다음 그림을 보겠습니다.

여기서는 어떤 interval도 서로 같지 않습니다. 그러므로 $Observation2$ 는 아무런 도움이 되지 않습니다. 다음의 lemma는 이보다 도움이 됩니다.
Lemma 4. If $ I_1,…, I_k$ is a partition of $I$ such that, for all $i = 1,…, k$, every pair of two intervals in $I_i $ intersects, we have $OPT(I) \le k$ .
$Proof.$ $O$ 를 optimal solution 이라고 해보자. 앞서 살펴봤듯이 하나의 partition과 $O$ 는 겹치는 interval은 최대 1개이다.왜냐하면 한 partition 안에서는 모든 interval들끼리 incompatible 하기 때문입니다. 즉 한 partition 안의 interval들은 서로 모두 겹친다는 의미입니다. 그렇게 겹치게끔 partition을 만듭니다. 따라서 각 $k$개의 partition들이 $O$ 와 겹치는 것을 모두 합해봤자 $k$ 입니다.
| $OPT(I)= | O | =\sum^k_{i=1} | I_i \cap O | \le k$. |

위 그림을 보면 하나의 partition 안에 있는 interval끼리는 모두 겹칩니다. 그러므로 한 partition 안에서 $O$ 와 겹치는 것은 최대 1개입니다. 그러므로 partition을 잡을 때는 반드시 안에 있는 모든 interval들끼리 incompatible해서 $O$와 겹치는 것이 최대 1개가 되도록 해야 합니다. 이제 정리를 해보겠습니다.
정리
마지막으로 instance $I’’’ $로 하나의 예시를 더 들고 글을 마치겠습니다.

이런 instance가 있을 경우 아래와 같은 예시 하나를 보여주면 바로 lower bound를 잡을 수 있습니다, $OPT(I’) \ge 3$ .
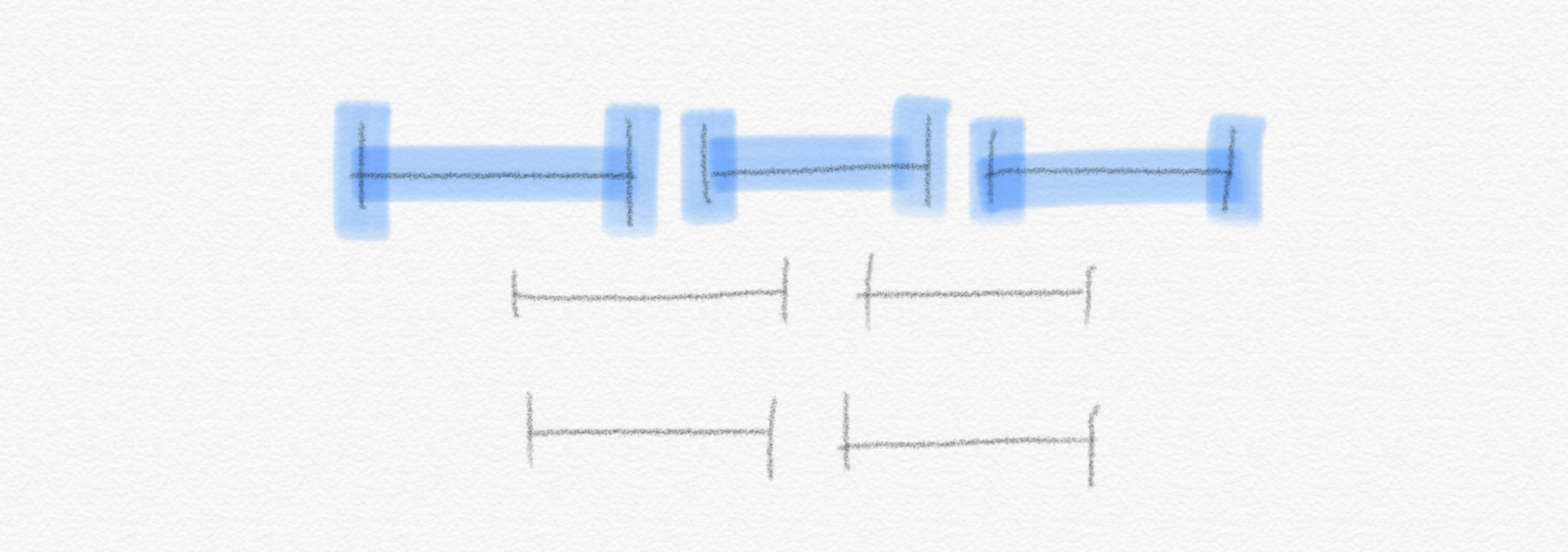
그리고 upper bound는 이런 partition이 존재한다는 사실을 보이면 잡을 수 있습니다, $OPT(I’) \le 3$ .
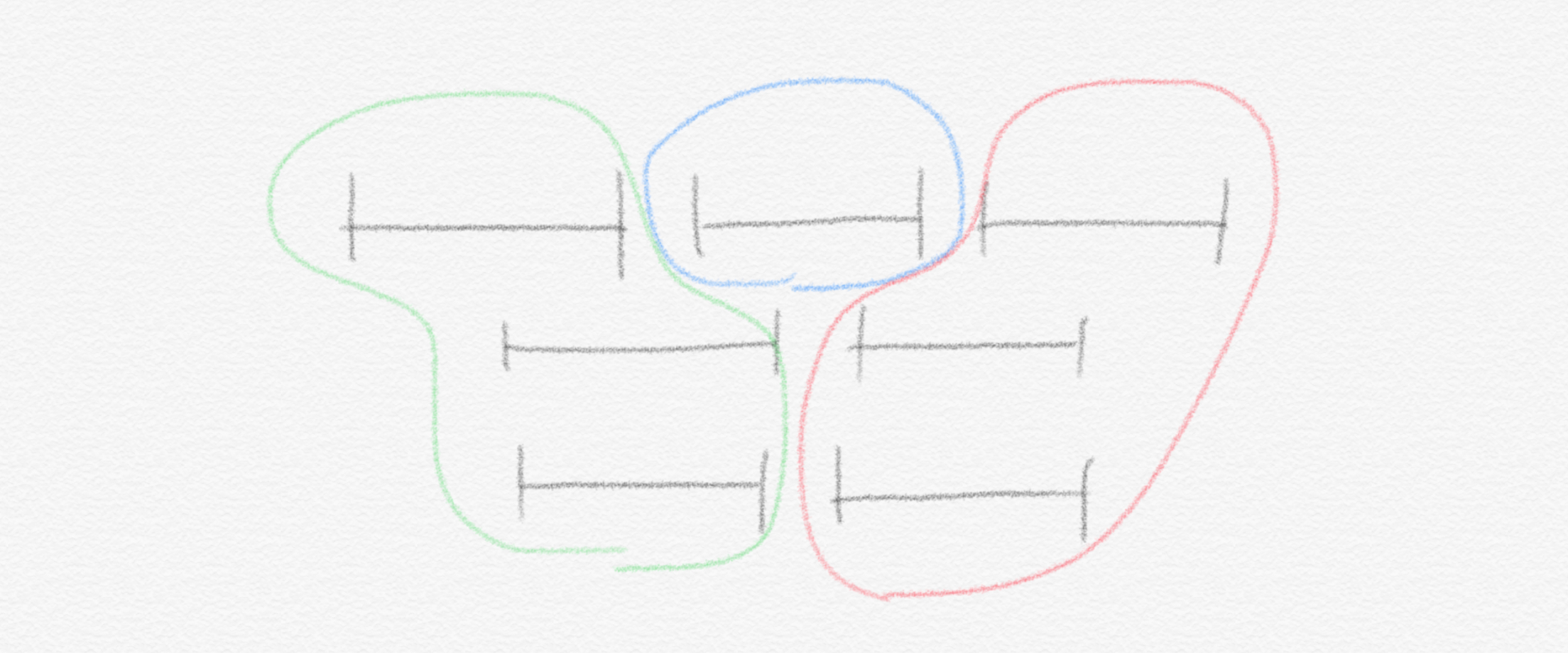
그림을 보면 각 partition 안의 interval들은 서로 모두 incompatible 하다는 사실을 알 수 있습니다. Lower bound가 3이고, upper bound도 3이므로 우리는 $OPT(I’’’)=3$ 임을 certificate을 이용하여 증명하였습니다.
다음 글에서는 또다른 greedy algorithm의 증명방법인 Exchange argument에 대해 다루겠습니다.
- Algorithm Analysis - Greedy Algorithm 1 SERIES 1/3
- Algorithm Analysis - Greedy Algorithm 2 ✓ SERIES 2/3
- Algorithm Analysis - Greedy Algorithm 3 SERIES 3/3