Algorithm Analysis: NP problems 1
알고리즘 관련 모든 글은 연세대학교 안형찬 교수님의 CSI_3108: Algorithm Analysis의 강의 내용과 자료입니다.
컴퓨터과학에서 어떤 문제를 효율적으로 푼다는 것은 해당 문제를 polynomial time에 푸는 것을 의미합니다. 그런데 효율적으로 푸는 방법을 모르는 문제들(polynomial time 안에 푸는 방법을 아직 모르는 문제들)이 발견되기 시작했습니다. 여기서 이 ‘푸는 방법을 모르는’ 부분에는 2가지 가능성이 존재합니다.
- 그 문제를 polynomial time에 푸는 알고리즘이 존재하지만 단지 우리가 아직 그것을 발견하지 못 한 것일 수 있습니다.
- 실제로 그 문제를 polynomial time에 푸는 방법이 존재하지 않을 수 있습니다.
이렇게 우리가 당장은 polynomial time에 푸는 알고리즘이 없는 문제들을 “어려운” 문제로 분류하기 시작했습니다. 그런데 어떤 문제가 다른 문제들보다 어렵다는 것을 말로는 대략 설명할 수 있지만 이를 어떻게 명확하게 보일 수 있을까에 대한 고민도 시작되었습니다. 어떤 문제가 다른 문제에 대한 상대적 난이도를 엄밀하게 규정하고자 하였습니다. 여기서 등장하는 것이 Polynomial-time reduction입니다.
본격적으로 이에 대해 논의를 하기에 앞서 지금부터 다루는 문제들은 앞서 봤던 문제들과는 약간은 성격이 다르다는 점을 짚고 넘어가고 싶습니다.
Decision problem
지금까지 봐왔던 문제들은 Optimization problem입니다. 예를 들어 “이러쿵 저러쿵한 문제에서 어떤 k의 최댓값을 구하시오”와 같은 optimization 형식이었습니다. 하지만 지금부터 이야기 하는 ‘문제’는 Decision problem을 뜻합니다. 예를 들어 “이러쿵 저러쿵 문제에서 최대 k개의 어떤 무언가를 구할 수 있는가” 입니다. 따라서 답은 yes/no 형태입니다. 좀더 구체적인 예시로는 앞서 살펴봤던 interval scheduling 문제를 각각 optimization 형태와 decision 형태로 표현해보겠습니다.
- Optimization problem: 모든 스케줄들을 겹치지 않게 최대 몇 개까지 소화할 수 있는가?
- Decision problem: 최소 5개의 스케줄을 겹치지 않게 소화할 수 있는가?
그런데 사실 이 두 가지 버전은 크게 다르지 않습니다.
만약 우리가 optimization problem을 풀 수 있는 방법이 있다면, 우리는 decision problem 버전에 대해 쉽게 바로바로 풀 수 있습니다. 예를 들어, 모든 스케줄을 겹치지 않게 최대 6개까지 소화할 수 있는 문제였다면, 그 문제에 대한 decision problem들은 이 6을 기준으로 yes/no가 갈릴 것입니다. Decision problem이 “최소 4개의 스케줄을 겹치지 않게 소화할 수 있는가?”라면 이는 당연히 yes가 답입니다. 만약 “최소 9개의 스케줄을 겹치지 않게 소화할 수 있는가?”가 문제였다면, 이는 no가 됩니다. 왜냐하면 우리는 optimization problem의 답에 따르면 해당 문제에서는 최대 6개까지만 소화 가능하므로, 9개의 스케줄을 소화하는 것을 불가능하기 때문입니다. 반대로 우리가 해당 decision problem 버전을 다 풀어서 주어진 interval scheduling 문제에서는 7개를 기준으로 답이 yes와 no로 갈린다고 하면, optimization 버전의 답은 7이 되는 셈입니다.
앞으로 NP problem 관련 글에서 이야기하는 문제들은 모두 decision problem 이라고 간주하면 됩니다. 하지만 여기서 끝나는 것이 아닙니다. 재미있게도 problem이란 또 무엇인가에 대해 좀더 엄밀하게 정의를 해야 추후 논의에서 좀더 편해집니다.
Problem
뜬금없이 Problem이란 무엇인가라고 묻는다면 정말 이보다도 더 추상적인 질문도 없을 것 같습니다. 하지만 앞으로의 논의를 더 잘 이해하기 위해서는 이에 대해 명확히 정의내릴 필요가 있습니다.
Definition 1. We define an abstract problem $Q$ to be a binary relation on a set $I$ of problem instances, and a set $S$ of problem solutions, $Q \subseteq I \times S$ .
[CLSR 참조]
Problem이란, problem instance들의 집합과 problem solution들의 집합 간 이항관계(binary relation)입니다. Decision problem인 경우에는 Problem $Q$ 란, $Q$의 instance들의 집합인 $I$ 와 problem solution는 1, 0 ($=$ yes instance, no instance) 의 경우밖에 없으므로 ${1,0}$ 간 이항관계가 되겠습니다.
이렇게 말하면 무슨 말인지 더 와닿지 않을 수 있습니다. Binary relation(이항관계)이 무엇인지 먼저 살펴보아야 하나, 보다 직관적인 설명을 위해 예시를 보이고 넘어가겠습니다. ($\times$ 는 cartesian product를 뜻합니다.)
Minimum Spanning Tree(MST)를 생각해보겠습니다. Problem $Q_2$는 ‘최대 cost 3의 MST가 존재하는가?’ 입니다. Decision problem이므로 solution은 1, 0 둘 중 하나입니다. 따라서 이런 decision problem은 instance 집합 $I$ 를 solution 집합 $S$ 에 매핑시키는 함수와 같습니다.
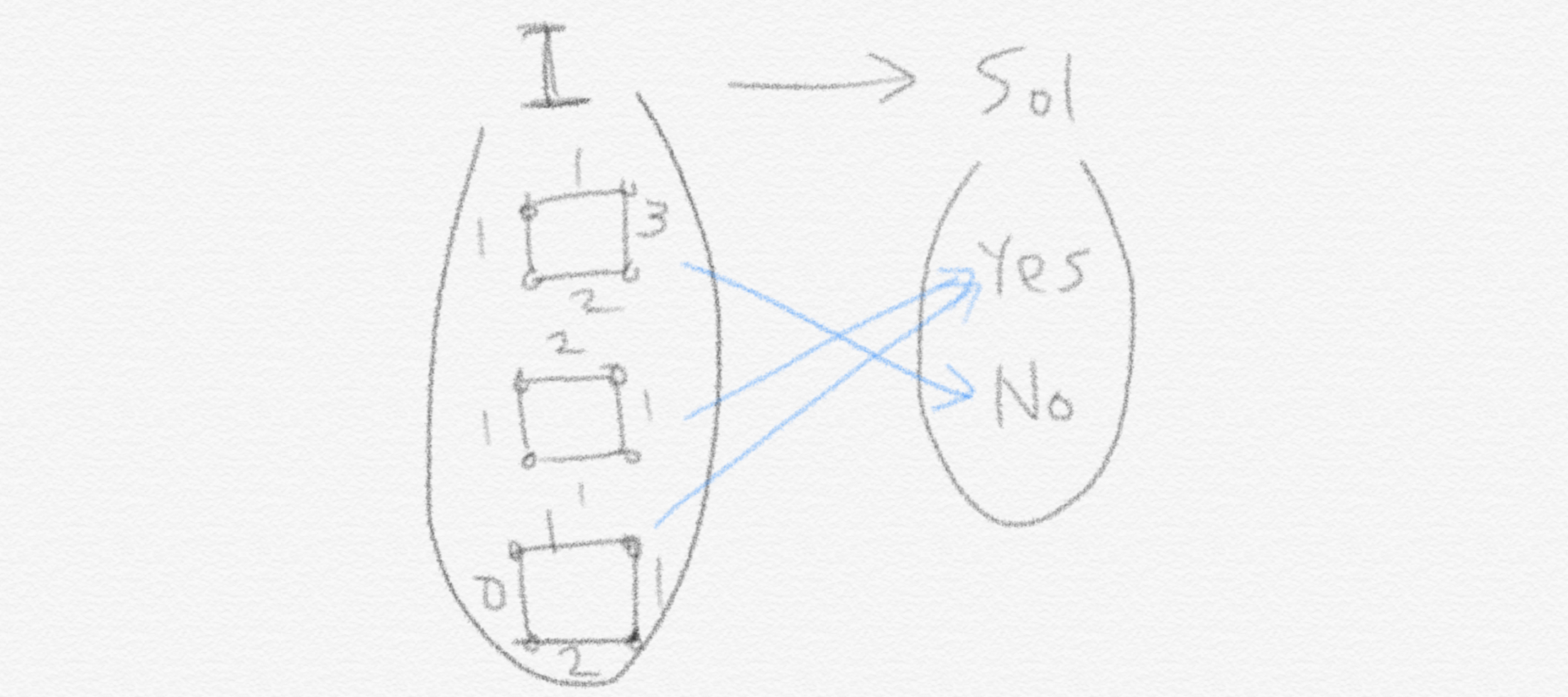
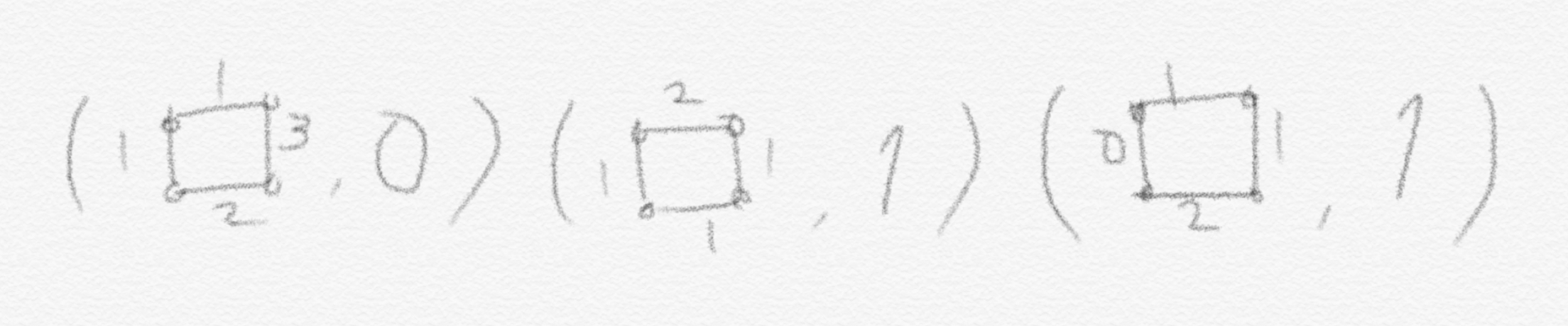
따라서 binary relation로 Problem $Q_2$는 이런 식으로 표현됩니다.
Problem $Q_3$는 ‘MST를 구해라’ 입니다. Solution은 우리가 평소 알던대로 구해진 MST가 됩니다.
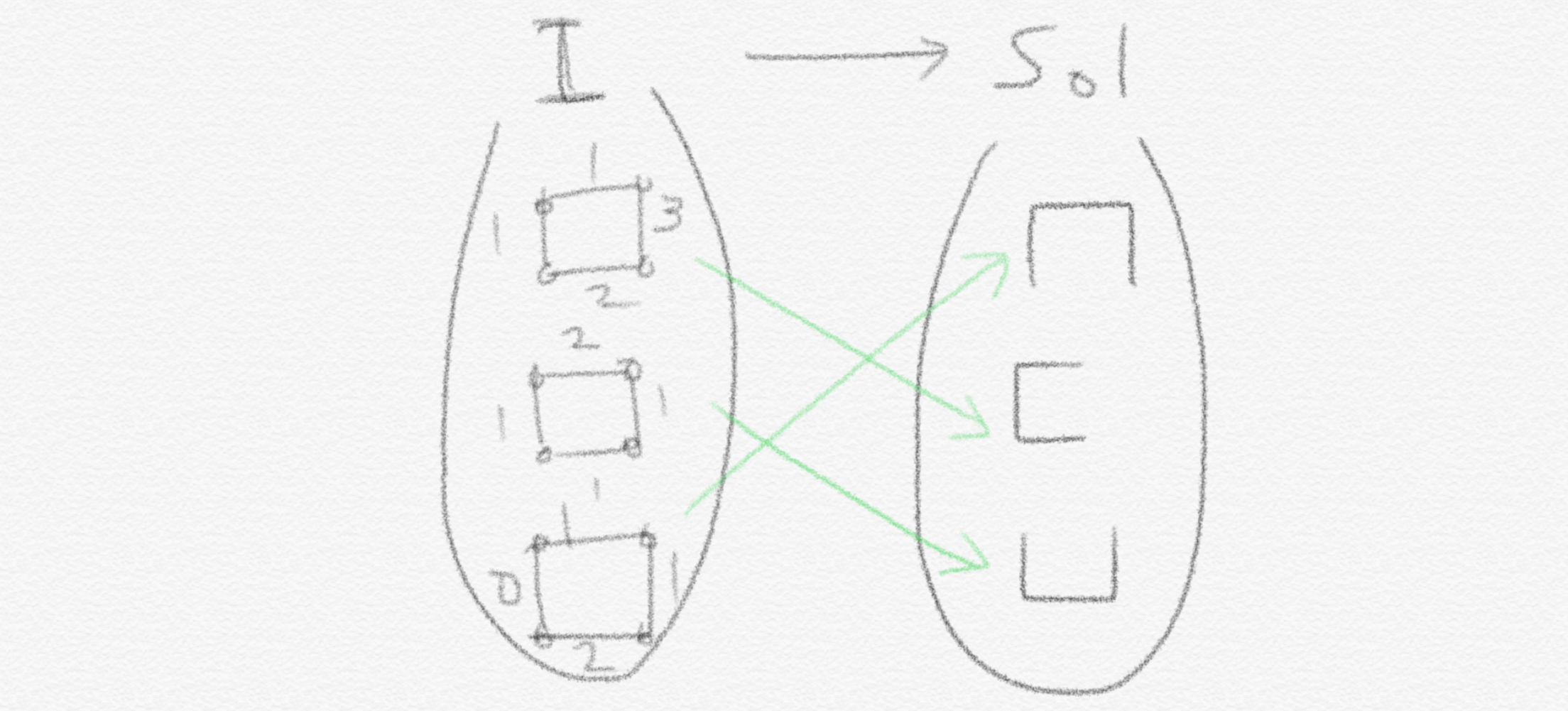
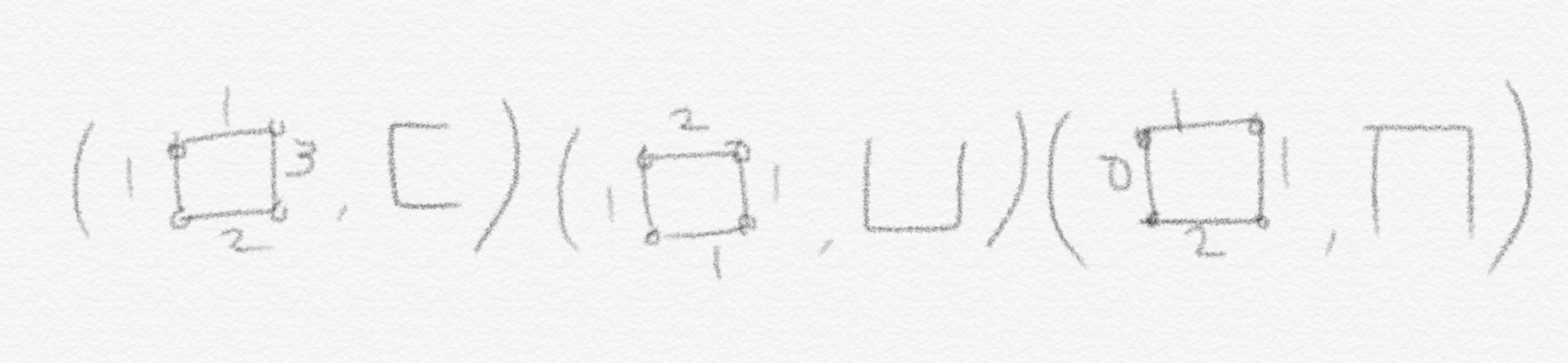
이렇듯 우리는 평소 어떤 problem의 instance가 주어지고 그에 매칭되어 있는 답을 찾기 위해 문제를 풀어왔던 것입니다.
Polynomial-time reduction
혼동을 피하고자 미리 밝히는데 polynomial-time reduction이 가능하다는 것은 어떤 문제를 polynomial time(즉, 효율적으로)에 풀 수 있다는 것과는 다른 이야기입니다. 우선 이해를 돕기 위해 예시 하나를 보겠습니다.
만약 우리가 어떤 수학 문제 $X$를 풀 수 있는 능력이 있을 때, 다른 수학 문제인 $Y$도 풀어낼 수 있다고 생각해보겠습니다.
이런 상황이라면 문제 $X$ 가 $Y$ 보다 쉽지는 않을 것입니다. 왜냐하면 $X$ 가 $Y$ 보다 쉬운 문제였다면, $X$ 를 풀 능력이 있다고 그 능력으로 $Y$ 도 풀어낼 수 있다는 보장은 없기 때문입니다. 누군가 수능 수학 문제를 풀 때 고난도 4점짜리 문제를 풀 수 있다고 한다면, 그 사람이 쎈수학 기본 개념 문제 정도는 그냥 풀 수 있을 거라고 예상하는 것은 자연스럽습니다. 하지만 반대로 쎈수학 기본 개념 문제를 풀 능력이 있다는 사실이, 수능 고난도 4점짜리 문제를 푸는 것을 보장해주진 않습니다. 그러므로 어떤 문제 $X$ 를 풀 수 있을 때 문제 $Y$ 도 풀 수 있다면, 적어도 문제 $X$ 가 문제 $Y$ 보다 쉽지는 않다는 것을 알 수 있습니다.
이제 본격적으로 polynomial-time reduction이 무엇인지 정의해보겠습니다.
Definition 2. Suppose we have a black box that solves any given instance of $X$. That is, if we write down an instance of $X$ and ask the black box, it returns the correct answer in a single step. If there exists an algorithm that, given any instance of $Y$ , solves the problem using a polynomial number of elementary operations in addition to a polynomial number of blackbox calls, we say $Y$ is polynomial-time reducible to $X$, denoted as $Y\le_p X$.
우리가 예시에서 봤던 그 X를 풀 능력이 있다는 부분이 바로 주어진 X instance를 바로 푸는 블랙박스가 있다는 부분에 대응됩니다. 우리에게 $X$ instance 를 한 번에 딱 바로 풀어버릴 수 있는 블랙박스가 있다는 것을 우선 전제로 합니다. 그리고는 $Y$ instance 를 polynomial time 안에 $X$ instance 형태로 바꾸고는 이렇게 나온 $X$ instance 꼴을 그 블랙박스가 딱 한 스텝에 풀어버릴 수 있다면 $Y$ 는 $X$ 로 polynomial-time reducible 한 것입니다, $Y\le_p X$.
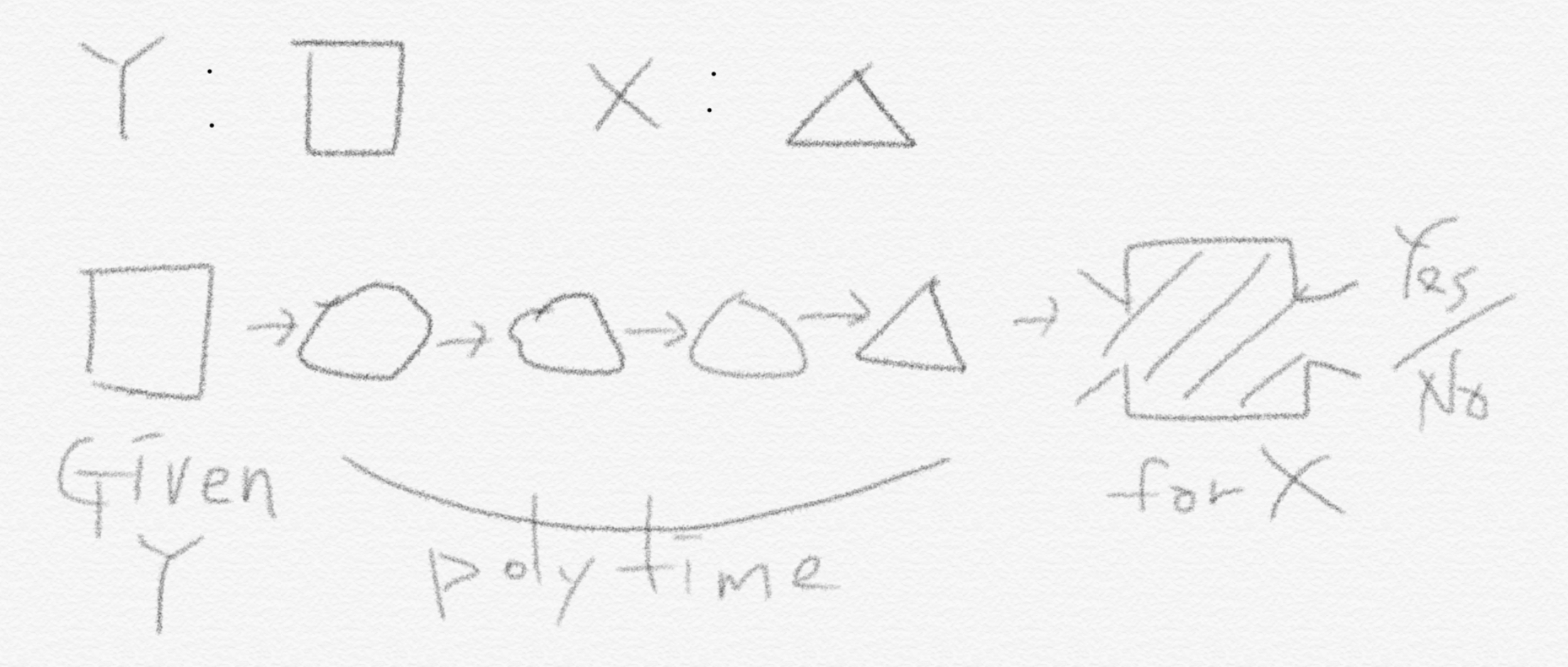
이런 상상 속의 블랙박스가 존재한다는 가정은 그냥 가정일 뿐입니다. 따라서 $Y$를 $X$ instance로 바꿀 수 있으면 무조건 풀립니다. 그러므로 이 개념에서 정말로 중요한 것은 주어진 $Y$ instance를 polynomial time 안에 $X$ instance 형태로 바꿀 수 있는지 여부입니다. 바꿀 수 있는지도 중요하지만, 바꿀 수 있더라도 그것이 polynomial time 안에 가능해야 합니다. 그리고 형태만 $X$ instance로 바꾸는 것이지, 답까지 바꾸는 것은 아닙니다. 따라서 바뀌기 전 $Y$ 형태의 instance가 Yes instance일 때(decision problem의 답이 yes라는 뜻입니다) 바뀐 후의 $X$ instance도 Yes instance여야 합니다. 그리고 당연히 $Y$ 형태의 instance가 No instance일 때는 $X$ instance도 No instance여야 합니다.
하지만 $y$ 가 False 일때의 논의는 대우명제로 바꿔서 보일 수 있습니다. $x =Yes \Rightarrow y=Yes$ . 실제 문제에서는 이것이 더 편하므로 이를 이용하겠습니다.
이렇게 적절히 형태를 바꾸고는 블랙박스가 X를 풀 게 되는 것입니다. 그렇다면 위 예시에서 봤듯이 $X$ 를 풀 수 있는 블랙박스가 있었기 때문에 $Y$ instance를 $X$ instance로 바꾸어서 풀어낼 수 있었습니다. 결국 $X$를 풀 수 있었기 때문에 $Y$도 풀 수 있었던 것이기 때문에, $X$가 더 어려운 문제입니다. 이를 정리해보겠습니다.
Theorem 1. Suppose $Y\le_p X$ . If $X$ can be solved in polynomial time, so can $Y$ .
$Proof.$ 위에 있는 정의에서 봤듯이 $X$ 를 위한 블랙박스를 이용해서 $Y$ 를 푸는 알고리즘 $A$ 가 있습니다. 그런데 $X$ 를 polynomial time에 푸는 알고리즘 $B$ 가 있습니다.
이때 생각을 해보면 $Y$를 그 블랙박스로 풀기 위해서 polynomial time에 걸려서 문제를 $X$ 꼴로 변형시킵니다. 그리고는 저 위의 블랙박스 대신에 그 $X$ 를 푸는 polynomial time에 푸는 알고리즘 $B$ 를 이용해서 문제 $Y$ 를 풉니다. 그러면 문제 변형에 polynomial time이 걸리고, 알고리즘 $B$ 를 이용해 푸는 데에 다시 polynomial time이 걸립니다. 따라서 도합 polynomial time + polynomial time 이 걸리게 되어 결과적으로 $Y$ 를 푸는데에도 polynomial time이 걸립니다. 따라서 위의 정리는 옳습니다.
그렇다면 이에 대한 대우 명제도 당연히 참입니다.
Corollary 1. Suppose $Y\le_p X$. If $Y$ cannot be solved in polynomial time, $X$ cannot be solved in polynomial time either.
언뜻보면 대우명제 참인 게 뭐 대수냐고 할 수 있습니다. 하지만 이 명제가 뒤에서 꽤 쓰입니다. 왜냐하면 이 명제는 이미 $Y$ 가 어렵다고 알려져있으면, $X$ 도 어려울 것이라는 사실을 알려주기 때문입니다. 이미 $Y$ 가 어렵다고 알려져있을 때, $Y\le_p X$ 를 보일 수 있다면, $X$ 도 어렵다는 사실을 알 수 있습니다. 이는 추후 NP-completeness 를 보일 때 써먹는 논리이므로 뒤에서 많이 다루게 될 예정입니다.
마지막으로 아래 lemma 가 polynomial-time reducibility는 transitive 하다는 사실을 말해줍니다.
Lemma 1. If $Z\le_p Y$ and $Y\le_p X$ , then $Z\le_p X$ .
$Proof.$ $X$ 를 푸는 블랙박스가 주어져있을 때, $Z$ 에 대해 $Y$ 를 푸는 블랙박스가 있는 알고리즘을 이용하고는 그리고는 그 $Y$ 로 바뀐 형태에 대해 $X$ 를 푸는 블랙박스가 있는 알고리즘을 이용하면 우리는 $Z$ instance 를 풀어낼 수 있습니다.

정리
효율적으로 풀지 못 하는 문제들이 존재합니다. 이에 대해 상대적 난이도라도 정해보고 싶습니다. 여기서 등장하는 개념이 polynomial-time reduction입니다. 어떤 문제 $X$ 를 풀 수 있는 능력이 있을 때, 다른 문제 $Y$ 를 풀 수 있다면, $X$ 가 더 쉽지는 않은 것입니다. 이를 $X$ 를 한방에 풀 수 있는 블랙박스가 있다고 가정해보고는 문제 $Y$ 를 $X$ 의 형태로 polynomial time 안에 변형시킵니다. 어떤 $X$ 의 특수한 꼴의 instance로 변형시키고는 두 가지 사실을 더 보여야 합니다.
- $y =Yes \Rightarrow x=Yes$
- $x =Yes \Rightarrow y=Yes$
이렇게 보이면 $Y\le_p X$ 임을 증명한 것입니다. 이제 개념 소개에 대해서는 여기까지 마치고 다음 글부터는 실제 문제 예시들로 이를 적용해보겠습니다.
덧
Polynomial-time reduction에 대해 저에게 누군가 적절한 그림을 알려준 적이 있는데 이를 빌려와봤습니다.
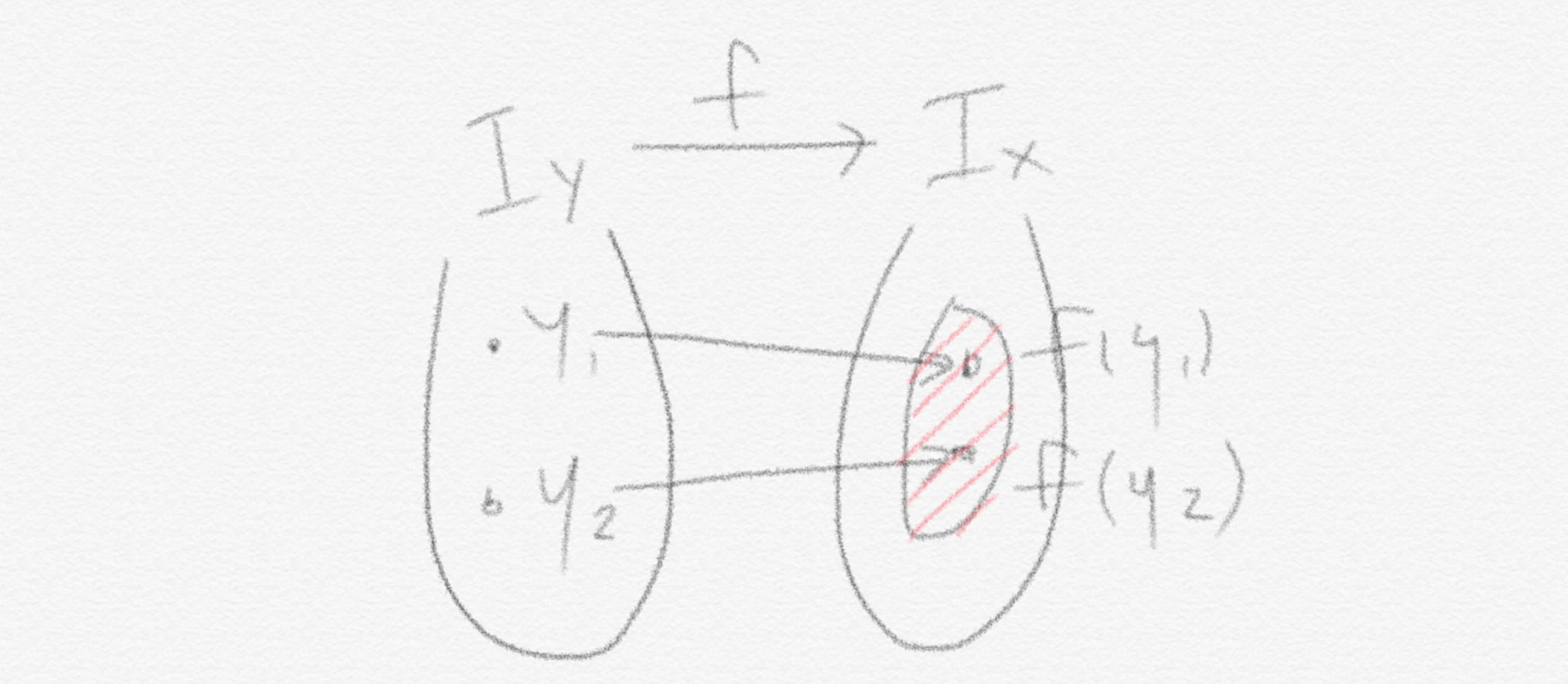
$Y$ instance 를 $X$ 꼴로 매핑을 시킬 것입니다. 하지만 우리는 어떤 특수한 $X$ instance로 변형을 하는 것이기 때문에, 그 특수한 애들(빨간 빗금 영역)만 신경쓰면 됩니다. 전체 $X$ instance를 신경쓸 필요 없습니다. 이 그림을 이용한 설명은 추후 문제를 살펴보면서 더 살펴보겠습니다.
- Algorithm Analysis - NP Problems 1 ✓ SERIES 1/5
- Algorithm Analysis - NP Problems 2 SERIES 2/5
- Algorithm Analysis - NP Problems 3 SERIES 3/5
- Algorithm Analysis - NP Problems 4 SERIES 4/5
- Algorithm Analysis - NP Problems 5 SERIES 5/5