Algorithm Analysis: NP problems 5
알고리즘 관련 모든 글은 연세대학교 안형찬 교수님의 CSI_3108: Algorithm Analysis의 강의 내용과 자료입니다.
지금까지의 이야기
지금까지 살펴본 바에 의하면 아래가 성립합니다.
이에 따라 Independent set과 Vertex cover는 동일한 난이도라는 사실을 알 수 있었습니다. 그리고 참고로 $VertexCover \le_p 3-SAT$ 임이 세상에 알려져있습니다. 따라서 3가지 문제는 모두 동일한 난이도를 갖습니다. 하지만 수 십 년 간 아무도 이 문제들을 polynomial-time에 푸는 알고리즘을 발견하지 못 했습니다. 꽤 어려운(hard) 문제라는 것이 짐작됩니다. 그러므로 이 3가지 문제를 어떤 다른 문제 $X$ 로 reduction이 가능하다면, $X$ 도 어려운 문제임을 알 수 있습니다. 이 3가지 문제들은 어려운 문제들의 대표격인데, 왜 대표격이냐면 이들이 어려운 문제 중에서도 가장 어려운(hardest) 문제들이기 때문입니다. 그렇다면 여기서 말하는 “어려운 문제”들의 집합과 “가장 어려운 문제”들의 집합을 정의해봐야 합니다.
위 3가지 문제의 공통점 중 하나는 이들이 yes instance 일 때, yes instance 임을 보이기(certify) 쉽다는 점입니다. 예를 들어 3-SAT 문제가 주어져있을 때, 제가 여러분에게 이것이 yes instance 임을 보이고 싶으면 그냥 만족하는 boolean 값 assignment를 여러분에게 주면, 여러분이 그것으로 3-SAT instance가 만족되는지 확인해보면 됩니다. 확인해서 만족하면 yes instance 인 셈입니다. 이렇게 단순히 그냥 답이나 힌트를 보여주면 됩니다.
하지만 해당 instance가 no instance임을 보이고 싶으면 어떻게 해야할까요? 제가 여러분에게 단순히 만족되지 않는 예시를 보여주는 것만으로 충분한가요? 전혀 아닙니다. 실제로는 만족하는 예시가 존재하는데, 단순히 제가 여러분에게 보여준 그 예시가 틀린 예시일 수 있는 것입니다. 그렇다면 해당 instance에서 가능한 모든 예시를 제가 여러분에게 보여드리고는 전부 만족되지 않는다는 것을 보이면 어떨까요? 이는 exponential 만큼의 예시가 존재하고, 이를 모두 확인하는 것은 너무나 오래 걸리는 작업입니다. 그러므로 이런 방법은 배제하겠습니다. 왜냐하면 언제나 그랬듯이 걸리는 시간이 중요하기 때문입니다. 그럼 이제 본격적으로 그 유명한 P, NP 에 대해 이야기할 준비가 된 것 같습니다.
P, NP
어떤 수학 문제가 있을 때, 그것의 해답이 23임을 딱 바로 찾아내는 것과 그것의 해답이 혹시 17인지 확인하는 것은 분명 다른 일입니다. 논의를 시작하기에 앞서 어떤 문제에 대한 해답(solution)을 찾아내는 것과 어떤 문제에 대해 제안된 답이 올바른 것인지 확인하는 것은 다른 작업이라는 점을 짚고 넘어가고 싶습니다.
지금부터는 주어지는 문제의 instance를 어떤 하나의 string $s$ 로 간주하겠습니다. 그리고 $|s|$ 는 해당 string의 길이를 나타냅니다.
P
Definition 1. We say $A$ is an efficient algorithm for problem $X$ if the following properties hold:
- $A$ takes a string $s$ as the input;
- the running time of $A$ is bounded by a polynomial in $|s|$;
- $A$ returns yes if and only if $s$ is a yes instance of $X$.
Efficient algorithm $A$ 는 우선 주어진 문제 $s$ 를 인풋으로 받습니다. 그리고 알고리즘 $A$ 의 시간복잡도는 $s$의 길이인 $|s|$ 에 대한 polynomial time 입니다. 그리고 $A$ 는 $s$ 가 yes instance 일 때만 $yes$ 라고 리턴합니다. 결국 그냥 decision problem인 $X$ 를 polynomial-time에 푸는 알고리즘이 $A$ 입니다(polynomial-time에 풀기 때문에 efficient algorithm이라고 합니다).
Definition 2. $P$ is the set of the (decision) problems for which there exists an efficient algorithm.
그리고 이렇게 polynomial-time에 (decision) 문제를 풀어내는 efficient한 알고리즘 $A$ 가 있는 문제들의 집합이 $P$ 입니다. 우리가 흔히 말하는 그 $P$/ $NP$ 문제에서의 $P$ 입니다. $P$ 는 집합이기 때문에 어떤 문제에 대해 polynomial time에 푸는 알고리즘이 있다면 그 문제는 $P$ 에 속한다고 표현합니다($X$ is in $P$).
NP
Definition 3. We say $B$ is an efficient certifier for problem $X$ if the following properties hold:
- $B$ takes two strings $s$ and $t$ as the input;
- the running time of $B$ is bounded by a polynomial in $|s|$ and $|t|$;
- there exists a polynomial function $p$ such that, for every yes instance $s$, there exists a string $t$ such that $|t| ≤ p(|s|)$ and $B$ returns yes on input $s$ and $t$;
- if $s$ is a no instance, $B$ returns no on input $s$ and $t$ for all $t$.
앞선 $P$에서와 달리 여기선 $s$만 갖고는 yes instance인지 판별할 수가 없고, 어떤 다른 certificate $t$가 같이 주어져야 합니다. 게다가 그 certificate이 올바른 것이어야 비로소 yes instance인지 판별할 수 있습니다.
직관적으로 설명을 해보면, efficient certifier는 올바른 힌트 또는 답이 주어졌을 때 yes instance를 구별하면서도 no instance일 때는 어떤 힌트나 답을 주어도 절대 yes instance라고 잘못 응답하는 일은 없는 프로그램입니다. 따라서 애초에 no instance인 경우에는 어떤 $s$나 $t$를 주어도 no라고 합니다. 만약 yes instance의 경우에 올바른 힌트를 주면 yes instance라고 알려줍니다.
Definition 4. $NP$ is the set of the (decision) problems for which there exists an efficient certifier.
따라서 이런 efficient certifier가 존재하는 문제들의 집합을 우리는 $NP$라고 합니다.
P와 NP의 관계
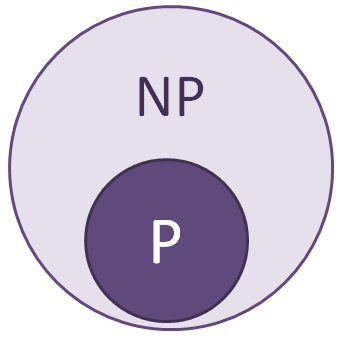
흔히 하는 오해 중 하나가 $NP$가 “not polynomial-time”인 줄 아는 것입니다. 하지만 이 오해가 얼마나 잘못되었는지는 아래 theorem을 보면 알 수 있습니다. $P$는 $NP$에 속합니다.
Theorem 1. $ P \subseteq NP$.
$Proof.$ 만약 어떤 $X$가 $P$에 속한다고 가정해보겠습니다: $X \in P$. 그렇다는 말은 $X$에 대한 efficient한 알고리즘 $A$가 존재한다는 것입니다. 그럼 우리는 이를 이용해 $X$에 대한 efficient certifier $B$도 만들 수 있습니다. 우리가 certifier에 넣을 $s$와 $t$를 준비해서는 인풋으로 $B$에 넣습니다. $B$는 이를 받아서 $t$를 버리고는 $s$를 efficient한 알고리즘 $A$에 넣습니다. 그러면 이제 앞서 살펴봤듯이 $A$는 이 $s$가 yes instance일 때만 $True$를 반환하기 때문에 이 $s$가 $True$면 $True$를 리턴해줍니다. 따라서 이 결과를 그대로 받아서 출력하는 $B$ 역시 $s$가 yes instance일 때만 $True$를 반환하게 됩니다. 결국 $B$는 $s$와 $t$가 주어졌을 때 polynomial-time에($A$가 polynomial-time에 돌고 $B$는 그 결과만 그대로 받아오면 되니) yes instance를 판별할 줄 아는 efficient한 certifier입니다. 그러므로 $P$는 $NP$이기도 합니다.
우리가 앞서 봤던 문제들에 적용해보기
- Independent set문제에 우리가 어떤 최소 k개의 특정 vertex들로 이루어진 집합이 바로 certificate $t$입니다. 이 vertex들이 정말로 edge를 두고 서로 인접하는지 체크해봅니다.
- 3-SAT 문제에서 특정 variable들에 True 또는 False 값을 매겨보고는 체크해보는 것입니다.
NP-hard & NP-complete
NP-hard와 NP-complete의 정의입니다.
Definition 5. We say a problem $X$ is $NP-hard$ if, for all $Y \in NP$, $Y \le_p X$.
Definition 6. We say a problem $X$ is $NP-complete$ if $X \in NP$ and $X$ is $NP-hard$.
이제 어떤 문제가 가장 어려운지 알게 되었습니다. 스스로가 $NP$에 속하면서 $NP$에 있는 다른 문제들이 모두 해당 문제로 polynomial-time reduction이 가능한 문제 $X$가 가장 어렵습니다. 그리고 우리는 이런 $X$를 $NP-complete$하다고 부릅니다.
Theorem 2. Suppose $X$ is $NP-complete$. We can solve $X$ in polynomial time if and only if $P = NP$.
$Proof.$ 만약 $P=NP$라면, $X \in NP = P$이므로 $X$는 polynomial-time에 풀립니다. 게다가 $NP-complete$의 정의에 의해 $X$로 모든 $NP$ 문제들이 polynomial-time reduction이 가능하므로 $NP$에 있는 문제들도 모두 polynomial-time에 풀립니다.
어떤 문제가 NP-complete함을 증명하기
이제 살짝 방향을 틀어서 어떤 특정 문제가 $NP-complete$함을 증명하는 방식을 살펴보겠습니다.
Theorem 3. (Cook-Levin). 3-SAT is $NP-complete$.
$Proof.$ 생략합니다. 증명은 생략하지만 이 명제를 언급하는 이유는 어떤 문제가 $NP-complete$함을 증명할 때 이 3-SAT을 starting point로 삼을 수 있기 때문입니다.
Lemma 1. Suppose that $Y$ is $NP-complete$. If $X$ is a problem in $NP$ such that $Y \le_p X$, $X$ is also $NP-complete$.
$Proof.$ $NP$에 속한 모든 $Z$들에 대해 $Z \le_p Y \le_p X$가 성립합니다. 그러므로 우선 $X$는 $NP-hard$합니다. 게다가 $X$가 $NP$에 속하기까지 하니 $X$는 $NP-complete$합니다.
정리
따라서 앞으로 어떤 문제 $X$가 $NP-complete$함을 보여야 할 때는, 이미 $NP-complete$하다고 증명된 다른 문제 $Y$를 이용하면 매우 편리합니다. 그리고는 우선 $X$가 $NP$에 속한다는 사실을 보입니다. 이에 대해서는 앞선 efficient certifier의 존재를 보이면 됩니다. 그리고는 $Y$가 $X$로 polynomial-time reduction이 가능하다는 사실을 증명합니다. 그러면 이에 따라 $X$도 $NP-complete$함을 증명한 것입니다.
- Algorithm Analysis - NP Problems 1 SERIES 1/5
- Algorithm Analysis - NP Problems 2 SERIES 2/5
- Algorithm Analysis - NP Problems 3 SERIES 3/5
- Algorithm Analysis - NP Problems 4 SERIES 4/5
- Algorithm Analysis - NP Problems 5 ✓ SERIES 5/5