Algorithm Analysis: NP problems 4

알고리즘 관련 모든 글은 연세대학교 안형찬 교수님의 CSI_3108: Algorithm Analysis의 강의 내용과 자료입니다.

SAT problem

이번 글에서는 이전에 다뤘던 문제들보다 살짝 더 복잡한 SAT 이라는 문제를 다뤄보겠습니다. 우선 몇 가지 정의부터 보고 가겠습니다.

Definition 1. Suppose we are given $n$ Boolean variables $x_1 , . . . , x_n$ . We call a variable $x_i$ or its negation $\bar{x}_i$ a literal. A clause is a disjunction of distinct literals $t_1 ∨ · · · ∨ t_l$ , where each $t_i$ is a literal. We say a clause has length $l$ if it contains $l$ literals.

A (truth) assignment is an assignment of Boolean values to the variables. We say that an assignment satisfies a clause if the clause evaluates to true under the Boolean logic, and that an assignment satisfies a collection of clauses $C_1 , . . . , C_k$ if it satisfies all $C_i$ . In this case, we call the assignment a satisfying assignment with respect to $C_1 , . . . , C_k$ , and that the collection $C_1 , . . . , C_k$ is satisfiable.

$x_i$ 들은 boolean 값을 갖는 변수들입니다. 그리고 그냥 일반 $x_i$ 또는 이것의 negation(not) $\bar{x}_i$ 를 하나의 literal 이라고 부릅니다. 이런 서로 다른 literal 들이 논리연산자 or ($∨$) 로 연결되어 있는 절이 clause 입니다. 따라서 이런 literal 중 하나만 $True$ 면 해당 clause 는 $True$ 가 됩니다. Negation 항은 $x_i$ 가 $False$ 일 때 $True$ 가 되어, 해당 negation 항을 포함하고 있는 clause 는 $True$ 가 될 것입니다. 아래는 예시입니다. Variable에 어떤 boolean 값이 할당되는지에 따라 literal의 값, 나아가 clause의 값이 결정됩니다.

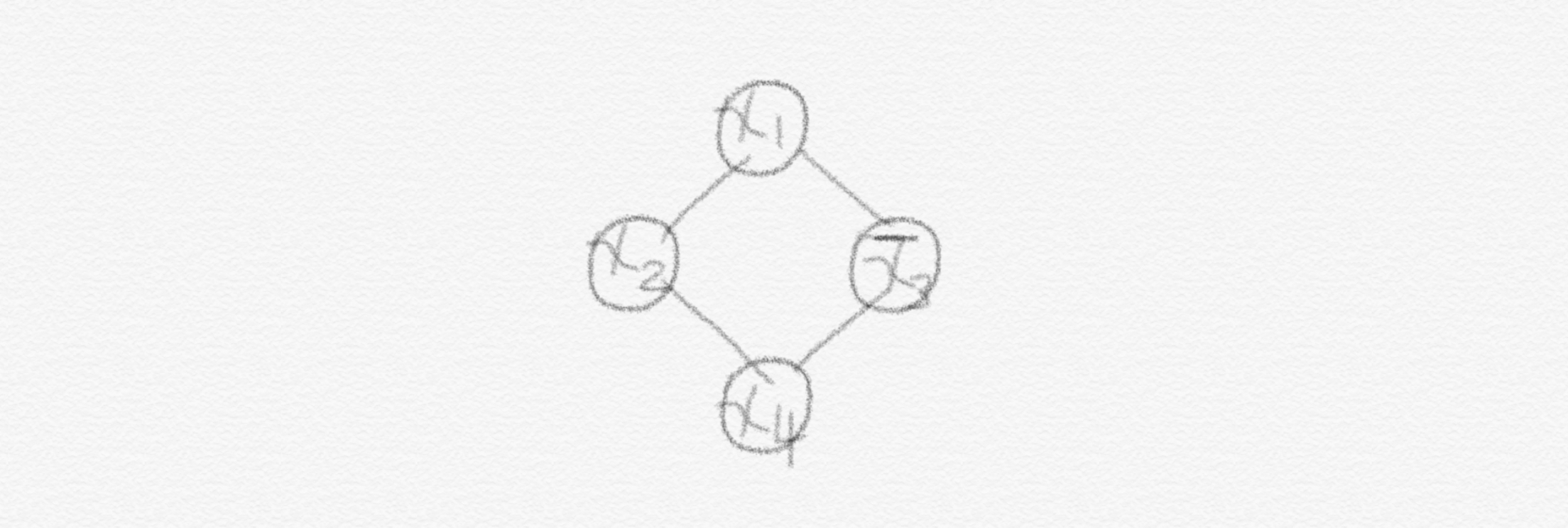
이런 clause 들이 $C_1, C_2 , … , C_k$ 이렇게 또 여러개 모인 collection이 존재합니다. Collection 안의 전체 clause 들이 모두 $True$ 가 될 때 해당 variable 들에 대한 assignment가 Satisfied 되었고, 해당 collection이 satisfiable 하다고 정의합니다. 결국 하나의 collection 은 clause 들이 and 논리연산자($\land$) 로 연결된 형태인 셈입니다.

SAT 문제는 아래와 같습니다.

Problem 1 (SAT). Given a set of $k$ clauses on $n$ variables, does there exist a satisfying assignment?

$n$ 개의 variable 들이 주어져있고($X={x_1, x_2, … , x_n}$), 그것들이 사용된 $k$ 개의 clause 들로 연결된 하나의 collection이 $True$ 가 되는 Satisfying assignment가 존재하는지 여부를 판단합니다. 그리고 SAT 문제 중에서 좀더 구체적인 3-SAT 문제를 살펴보겠습니다.

Problem 2 (3-SAT). Given a set of $k$ clauses on $n$ variables, each of length 3, does there exist a satisfying assignment? (We assume that each clause contains each variable at most once.)

일반적인 SAT 문제는 하나의 clause 가 몇 개의 literal 로 이루어져있는지에 대해 제약이 없습니다. 한 clause 는 12개의 literal 로 이루어져있을 수도 있고, 5개로 이루어져있을 수도 있습니다. 하지만 우리는 그 중에서 한 clause 에 오직 3개의 literal 만 있는 3-SAT 문제를 살펴보겠습니다. 그리고 한 clause 내에는 중복된 variable 이 존재할 수 없습니다. 이 말은, 한 clause 내에 $x_i$ 와 이의 negation 인 $\bar{x}_i$ 가 같이 있을 수 없다는 뜻입니다.

그런데 꽤 어려운 듯하게 보이는 이 문제는 사실 independent set 이랑 같은 난이도입니다. 같은 난이도를 보이려면 무엇을 해야 할까요? 양방향으로 polynomial-time reduction 을 시키면 됩니다. 하지만 여기서는 Independent set이 3-SAT 보다 더 쉽지 않다는 방향만 우선 보이겠습니다. 그 전에 정의 하나 먼저 살펴보고 증명을 시작하겠습니다.

Definition 2. We say two literals conflict if one is $x_i$ and the other is $\bar{x}_i$ , the negation of the other.

스포일러가 될 수도 있지만 $x_i$ 와 $\bar{x}_i$ 가 인접해 있으면 이를 conflict 라고 정의합니다.

Theorem 1. 3-SAT $\le_p$ Independent Set.

$Proof.$

이제 우리는 여태까지 해왔던 것처럼 Independent set 을 푸는 블랙박스가 있다고 가정해봅니다. 그리고 이 블랙박스를 활용하기 위해 주어진 3-SAT instance 로부터 Independent set instance 꼴을 만들어보겠습니다. 그리고 “Independent set instance가 yes instance $\iff$ clause collection이 satisfiable 하다”는 것을 보이겠습니다.

우선 $k$ 는 주어진 3-SAT instance의 clause 개수라고 하겠습니다. Independence set 은 그래프에서 vertex를 고르는 식의 문제였습니다. 따라서 우리는 3-SAT instance 를 이용해서 그에 상응하는 vertex 와 edge 로 인코딩하여 그래프를 그려야 합니다. 그렇게 하여 satisfying assignment가 존재한다는 사실이 그에 해당하는 그래프에서 큰 independent set의 존재한다는 사실과 대응되게 만들어야 합니다.

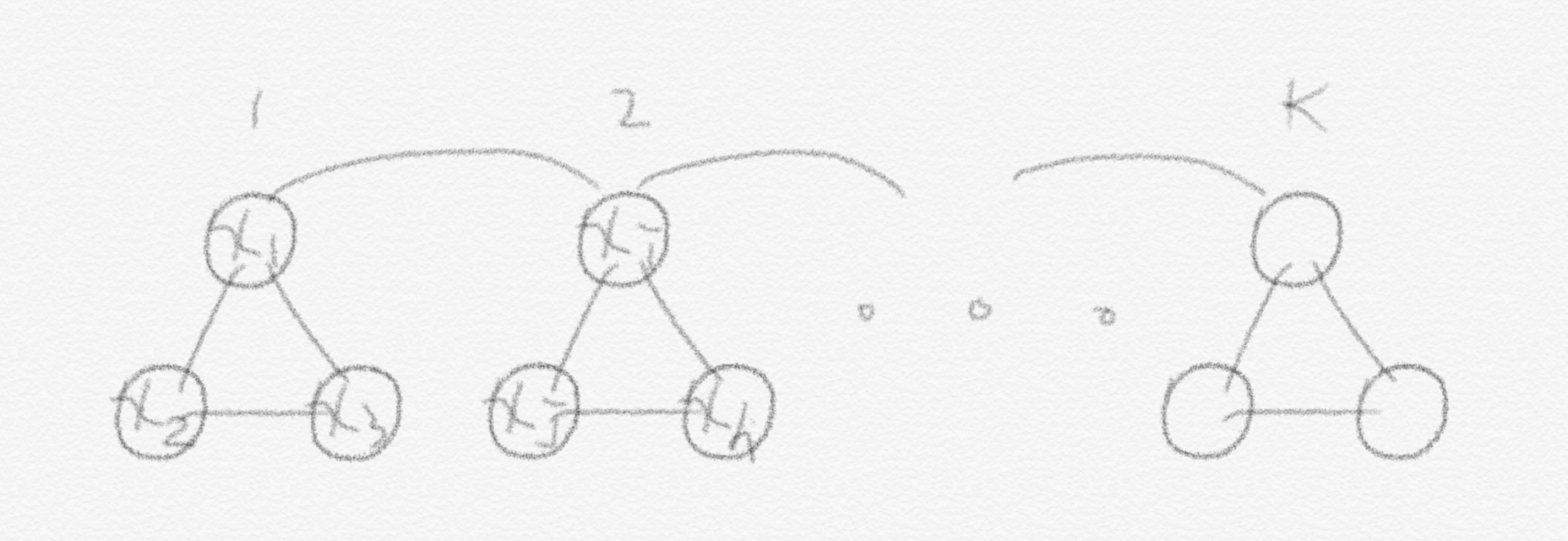
따라서 우리는 이제부터 vertex $3k$ 개짜리 graph $G=(V,E)$ 를 만들어보겠습니다. 3-SAT 에서는 한 clause은 오직 3개의 literal로 구성되어 있기 때문에 $3k$ 개짜리를 만듭니다. 한 clause를 이루는 3개의 literal들은 각각 하나의 vertex이고, 이 3개의 literal은 삼각형 모양으로 연결되어 있게 됩니다.

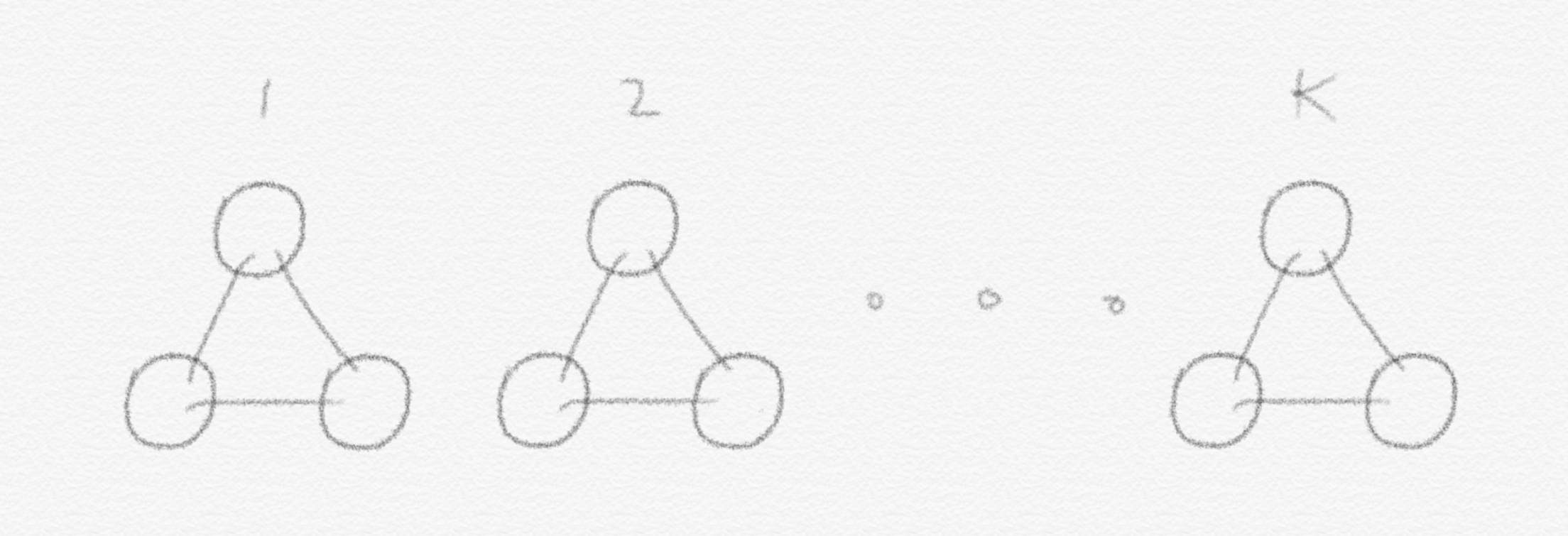
따라서 이런 삼각형이 $k$ 개 만들어집니다. 이런 삼각형들이 쭈욱 나열되어 있는 graph인 셈입니다. 이를 이용해서 해당 문제를 reduction 을 하기 위해서는 3-SAT 문제를 바라보는 2가지 관점이 존재한다는 사실을 알아야 합니다.

• 우선 그냥 단순하게 주어진 $n$ 개의 variable 에 각각 boolean 값을 할당하고 나서, 각 clause가 모두 $True$ 가 되면 그 3-SAT instance 는 satisfiable 한 것입니다.
• 또 다른 관점은, 각 clause에서 1개의 literal 씩 총 $k$ 개 뽑습니다. 그리고는 이렇게 뽑은 $k$ 개 literal 들을 모두 $True$ 가 되도록 boolean 값 할당이 가능하다면 해당 3-SAT instance 는 satisfiable 한 것입니다. 결국 관건은 $k$ 개의 literal을 잘 뽑는 것입니다. 뽑을 때 위 Definition.2에서 살펴본 conflict가 존재하지 않게 뽑으면 됩니다. 왜냐하면 뽑은 literal 중에 conflict가 존재하면 정의에 의해 둘 다 $True$ 가 될 수 없기 때문입니다. 따라서 conflict만 없게끔 literal들을 각 clause에서 뽑을 수 있으면 우리는 해당 instance가 satisfiable한 것입니다.

아래 그림을 보면 $k$개의 literal을 선택했는데, 거기에 $x_3$ 와 $\bar{x}_3$가 둘 다 뽑혔습니다. 이런 conflict을 피해서 우리는 $k$개의 literal을 뽑고 싶습니다.

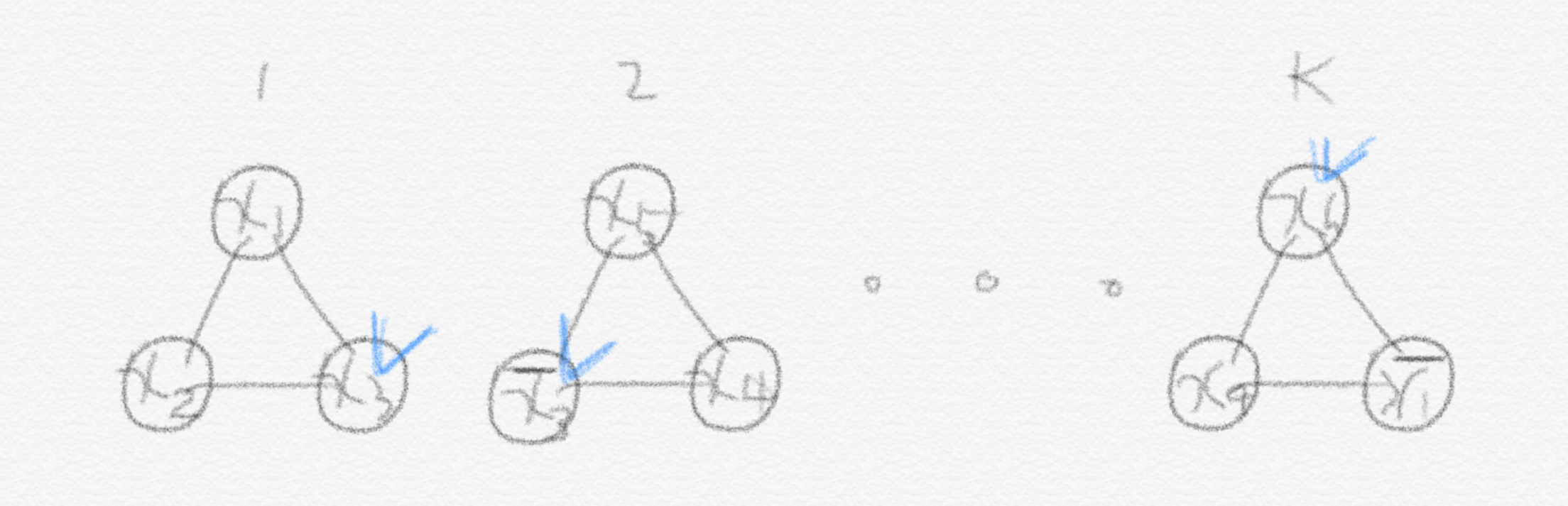
우리는 이제 저 2번째 관점을 이용해서 independent set으로 reduction을 시킵니다. 따라서 conflict 하는 쌍을 뽑지 않는 제약을 independent set 꼴에서 표현해야 합니다. 이를 위해서 앞서 만든 $k$개의 따로 떨어져있는 삼각형들에 edge를 추가로 그려줍니다. 아래와 같은 예시를 살펴보겠습니다. 어느 삼각형에 있는 literal 중에서 다른 삼각형에 conflict가 생기는 literal이 있다면 그것과 edge로 연결시킵니다. 다른 삼각형들에 conflict가 생기는 literal들이 있다면 한 literal에서 이 conflict edge를 여러개 연결시켜주면 됩니다.

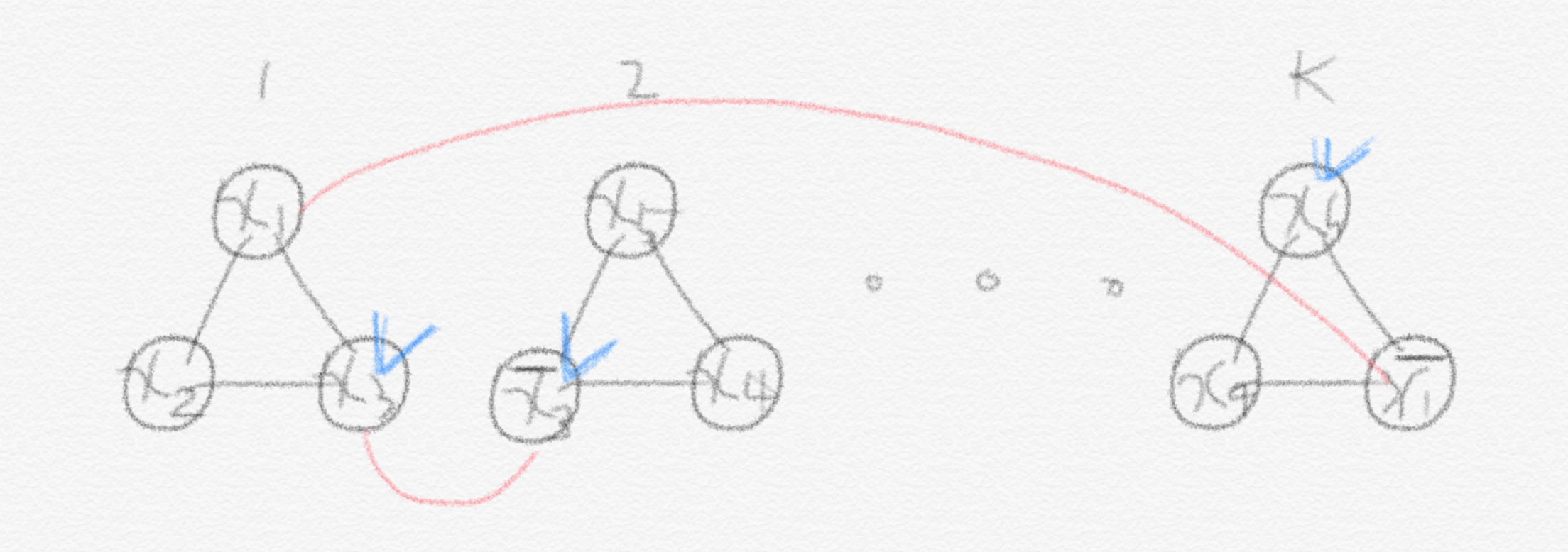
이렇게 construction 부분은 마무리가 되었습니다. 이제 한 꼴이 yes instance 일 때 다른 하나도 yes instance가 되는지를 보여야 합니다.

우선 3-SAT instance 가 satisfiable 하다고 가정해보겠습니다. 3-SAT instance가 yes instance 인 것을 가정하는 것입니다. 그러면 $k$ 개의 literal들을 $k$ 개의 clause로부터 conflict 없이 선택할 수 있었다는 의미가 됩니다. 그러면 그런 선택된 $k$ 개의 literal을 따라 만들어진 graph 에서 vertex를 선택하면 그 vertex들은 서로 independent 합니다. 왜냐하면 우리는 각 clause로부터 정확히 하나의 literal들을 뽑았으므로 graph 상에서 각 삼각형에서 하나씩 뽑은 셈이고, conflict 있는 쌍은 뽑지 않았으므로, 서로 edge로 연결되어 있지 않기 때문입니다.

이제는 반대로 해당 graph $G$ 에 최소 $k’=k$ 개인 independent set $S$가 존재한다고 가정해보겠습니다. 우선 $|S|=k$ 이므로, 각 삼각형으로부터 최대 1개의 vertex만 가질 수 있습니다. 한 삼각형을 이루는 vertex 3개는 모두 연결되어 있으므로 한 삼각형으로부터 2개나 3개를 가지게 되면 당연히 independent set이 될 수 없습니다. 이제 $S$ 에 있는 변수 $x_i$ 에 boolean 값을 할당하는 일만 남았습니다.

• 만약에 $S$ 에 literal $x_i$ 만 있고, $\bar{x}_i$ 는 없는 경우라면 변수 $x_i$ 에 $True$ 를 할당합니다
• 반대로 literal $\bar{x}_i$ 만 있고, $x_i$ 는 없는 경우라면 변수 $x_i$ 에 $False$ 를 할당합니다
• 만약 $S$ 에 literal $x_i$ 와 $\bar{x}_i$ 둘 다 없는 경우면 변수 $x_i$ 에 $True$ 를 할당합니다
• 덧붙여 말하면, $S$ 에 literal $x_i$ 와 $\bar{x}_i$ 둘 다 있는 경우는 존재할 수 없습니다. 왜냐하면 그런 literal들이라면 graph $G$ 상에서 conflict edge로 adjacent 했을 것이므로 independent 하지 않기 때문입니다.

이런 방법으로 boolean 값들을 할당하면, 각 삼각형에서는 하나의 vertex(즉, literal)만 선택되어 총 $k$ 개의 literal 들이 뽑혔을 것이고 모두 $S$ 에 있는 literal 들은 모두 결과적으로 $True$ 가 되므로 해당 3-SAT instance 는 satisfiable 하게 됩니다.

이런 construction(graph 를 만들어내는 일)은 단순히 그냥 literal $3k$ 개를 vertex로 만들고 edge로 이어주기만 하면 되는 작업이므로 polynomial-time에 가능합니다. 그러므로 주어진 3-SAT instance를 independent set을 푸는 black box를 이용해 polynomial-time 안에 풀 수 있음을 보였습니다.

정리

어떤 문제를 다른 문제로 reduction 시킬 때, construction 을 해야 합니다. 그런데 원래의 문제의 제약사항을 다른 문제에서 표현하기 위해 저희가 임의로 만들어주는 장치?들이 있습니다. 이를 Gadget이라고 부릅니다. 이번 문제에서는 conflict edge가 그 예시 중 하나입니다. Conflict edge 정도는 그냥 직관적으로 이해가 가므로 별 문제가 없지만, 다른 문제에서는 정말 말도 안 되게 복잡한 여러 gadget들을 만들어서 문제를 표현해야 하는 경우도 있습니다. 이런 gadget들을 잘 떠올릴 수 있으면 reduction을 잘 시킬 수 있습니다.

• Algorithm Analysis - NP Problems 1 SERIES 1/5
• Algorithm Analysis - NP Problems 2 SERIES 2/5
• Algorithm Analysis - NP Problems 3 SERIES 3/5
• Algorithm Analysis - NP Problems 4 ✓ SERIES 4/5
• Algorithm Analysis - NP Problems 5 SERIES 5/5

Algorithm Analysis