Algorithm Analysis: Greedy Algorithm 1

알고리즘 관련 모든 글은 연세대학교 안형찬 교수님의 CSI_3108: Algorithm Analysis의 강의 내용과 자료입니다.

이번 글에서부터는 모두가 익히 들어봤을 Greedy Algorithm에 대해 다루어보겠습니다. Greedy Algorithm이란, step마다 근시안적으로(myoptic) 현재에서 가장 좋은 것은 선택해 나아가는 알고리즘 방식입니다. 알고리즘을 떠올리는 아이디어도 중요하지만 Greedy Algorithm 파트의 글에서는 그 correctness를 증명하는 3가지 방식에 대해 중점을 두려고 합니다.

• the Greedy Algorithm stays ahead 방식
• Certificate 방식
• Exchange argument 방식

이 3가지에 대해서 문제를 풀며 설명을 하겠습니다. 우선 문제를 살펴보겠습니다.

Interval Scheduling

Suppose you are in charge of organizing the schedule of a lecture room. Given a set of room requests, you want to serve as many requests as possible. Each request is in the form of a time interval for which the room is requested, and you cannot serve two requests whose intervals overlap.

Let $n$ be the number of given requests, or intervals. We will represent each interval by a number in $I := {1,…, n}$. Let $s(i)$ and $f(i)$ respectively denote the starting time and finishing time of interval $i \in I$. We assume $s(i) < f(i)$ for all $i$.

Definition 1. We say two intervals $i$ and $j$ are compatible if either $f(i) \le s(j)$ or $f(j) \le s(i)$.

Definition 2. We say a set of intervals is compatible if every pair of intervals in the set is compatible.

We are now ready to formally state the problem.

Problem 1. Given a set of $n$ intervals $1,…,n$, find a maximum-cardinality subset of intervals that is compatible.

각 interval은 시작점 s(i)와 끝점 f(i)를 갖고 있고, 우리의 목표는 이런 interval들이 겹치지 않게(=compatible) 스케줄을 만들면서, 최대한 많은 interval을 소화하는 것입니다. 대략적인 절차는 간단하게 바로 생각이 납니다.

1. 남아있는 interval 중 하나를 받아들이고
2. 이 interval과 겹치는 interval들은 모두 지웁니다
3. 더이상 남은 interval이 없을 때까지 1~2번 과정을 반복합니다

관건은 interval을 뽑는 기준을 무엇으로 할지입니다. 생각해보면 몇 가지 방법이 바로 떠오릅니다. 최대한 많이 소화해야 하니까 가장 시작시간이 빠른 애들부터 차곡차곡 해치우는 방법, 아니면 최대한 안 겹치게 해야 하니까 소요시간이 가장 짧은 애들부터 고르는 방법 등이 있습니다. 아니면 다른 interval들과 가장 덜 겹치는 애들부터 하는 방식도 있습니다. 특히 최대한 안 겹치는 애들부터 소화해나가는 방법은 꽤나 그럴듯하게 보입니다. 하지만 이런 알고리즘은 아래와 같은 interval set이 주어졌을 때 최적의 답을 찾아내지 못 합니다.

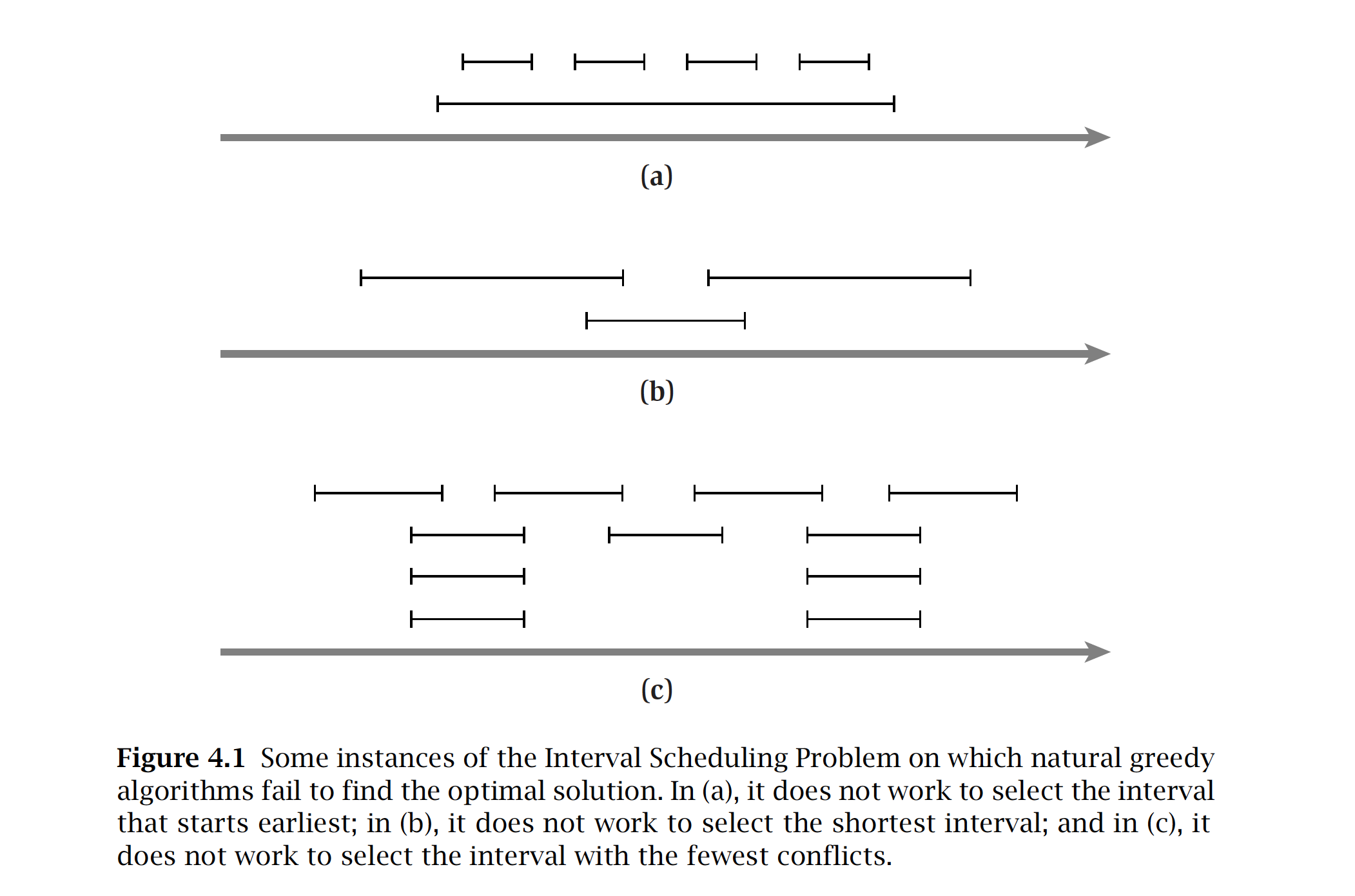
언뜻 쉬워보이는 문제지만 바로 optimal한 알고리즘인지는 알 수 없고, 이렇게 counter example들로 찾아나서야 합니다. 가장 빨리 끝나는 interval부터 해치운다 는 알고리즘은 어떨까요?

Algorithm

주어진 intervel set, R
sol = {}
while R!=empty:
	R에서 가장 빨리 끝나는 interval i를 고릅니다
	sol에 넣어줍니다
	R에서 i랑 겹치는 애들을 다 지우고, i도 지웁니다

직관적으로 최대한 뒤의 시간을 비워두는 전략입니다. 아래 그림을 보면 알겠지만 이 알고리즘은 사실 optimal solution을 찾아냅니다. 이제부터 그것에 대한 증명을 해보겠습니다. 사실 Greedy Algorithm은 아이디어도 중요하지만 여기서 중점적으로 다루려는 것은 Greedy Algorithm의 증명에 대한 접근방식에 익숙해지는 것에 더 중점을 둡니다. 우선 the Greedy algorithm stays ahead 방식을 해보겠습니다.

우선 가장 중요한 건 우리의 알고리즘이 compatible한 interval set을 반환하는지 여부를 보여야 합니다. 언뜻 너무 당연한 거라서 언급해야 하냐고 물을 수 있겠지만, 그런 당연한 절차를 명쾌하게 보이는 것이 알고리즘 증명에 중요합니다. 왜냐하면 주어진 문제에서 compatibility를 요구하기 때문입니다.

Observation 1. 이 알고리즘은 compatible한 interval들의 집합을 리턴한다.

$Proof.$ 알고리즘에서 매 단계마다 sol 집합에 넣은 interval과 incompatible한 interval들을 지운 상태에서 그 다음 interval을 고른다.

우선 우리의 알고리즘이 반환한 interval의 개수를 $k$라고 하겠습니다. 그리고 $i_l$ 이 $l$ 번째 iteration(위의 while문)에 선택된 interval을 뜻합니다. 그러니까 우리의 정답은 $sol={i_1, … ,i_k}$ 이런 형태일 것입니다. 그리고 optimal solution $O$가 있다고 가정하겠습니다. $O={ j_1, … , j_m }$, 그러니까 optimal solution의 interval 개수는 $m$ 입니다. 당장 마음 같아서는 $sol = O$ 임을 보이고 싶지만, optimal solution은 여러 개일 수 있습니다. 그리고 우리 알고리즘이 리턴한 $sol$은 아마 그 중 1개랑 같을 것입니다. 그래서 당장 $sol = O$ 임을 보이기는 어렵습니다.

그대신 어차피 주어진 문제는 interval 개수를 최대화하는 거에 관심이 있습니다. 따라서 $|sol|=|O|$ 임을 보여서 $sol$ 역시도 optimal 함을 보이면 됩니다. 우리의 greedy algorithm이 매 step에서 optimal $O$ 보다 앞서있다는 사실을 보이는 것입니다.

the Greedy-stays-ahead

Lemma 1.

$1 \le r \le m$ 을 만족하는 모든 $r$에 대해서 $f(i_r) \le f(j_r)$ 가 성립한다.

이 말을 쉽게 풀어쓰면, 각 모든 단계에서 우리의 알고리즘이 고르는 interval이 optimal한 애가 고르는 interval보다 finishing time이 느리진 않다는 의미입니다. 우리 알고리즘이 고르는 interval이 optimal이 고르는 애보다 앞서있다고 말하고 싶은 것입니다.

$Proof.$

귀납법으로 증명하는 것이 가장 자연스러워 보입니다. $r$ 에 대한 귀납법으로 시작하겠습니다. 우선 $r=1$일 때 $f(i_1) \le f(j_1)$ 인 것은 너무나 뻔합니다. 왜냐하면 우리 알고리즘에서 가장 빨리 끝나는 interval을 고르고 시작하기 때문입니다.

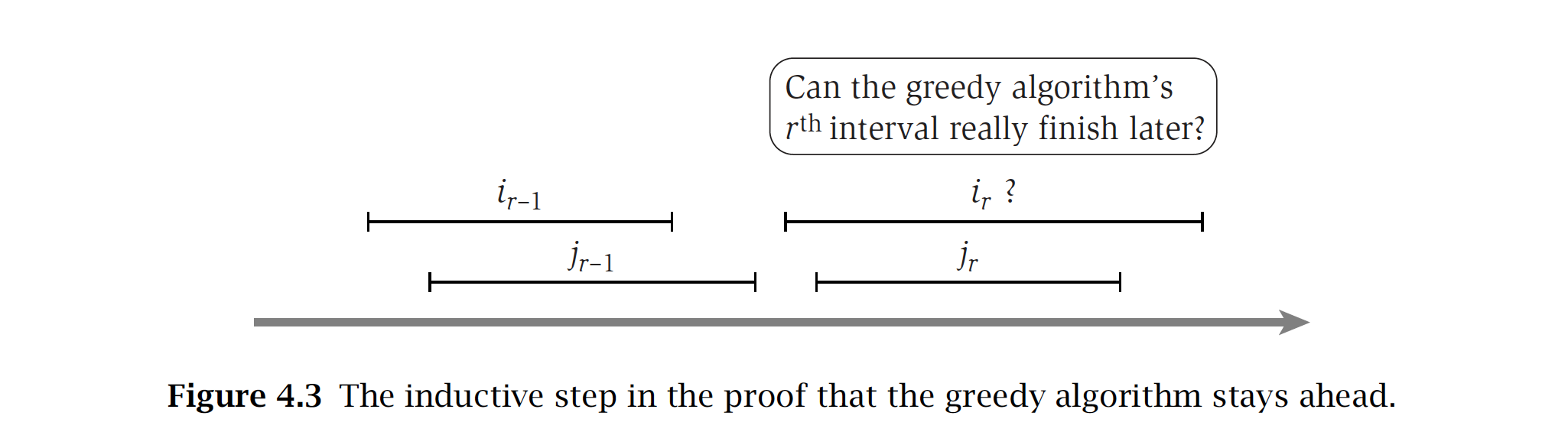
이제 $r \ge 2 $ 일 때를 생각해보겠습니다. 귀납법을 이용한 증명에서 늘 하듯이, $f(i_{r-1}) \le f(j_{r-1})$ 이 참이라고 하면 $f(i_r) \le f(j_r)$ 도 참이라는 것을 증명하는 방식입니다. $f(i_{r-1}) \le f(j_{r-1})$ 이 참이라고 가정하겠습니다. 우선 optimal한 $O$ 는 당연히 compatible 한 interval들로만 이루어져있을 것입니다. 그러므로 $f(j_{r-1}) \le s(j_{r})$ 이 참일 것입니다. $O$에서는 r-1번째 interval이 끝나는 시간과 r번째 interval이 시작하는 시간은 서로 overlap되지 않을 것이라는 의미입니다. 우리가 방금 참이라고 가정했던 $f(i_{r-1}) \le f(j_{r-1})$ 을 이용해보면 결국 $f(i_{r-1}) \le f(j_{r-1}) \le s(j_{r})$ 이 됩니다. $j_r$ 의 interval은 우리 알고리즘이 고른 (i-1)번째 interval의 끝나는 시간 이후에 시작한다는 의미입니다. 결국, 우리 알고리즘이 i-1번째 interval을 고른 후에도 그 $j_r$ 의 interval은 우리 선택지에 남아있음을 뜻합니다(intersect하지 않으니 $R$에 남아있게 됩니다). 이렇게 $j_r$ 의 interval이 우리의 선택지에 남아있음에도 불구하고 우리의 알고리즘이 $i_r$ 의 interval을 골랐다는 것입니다. 그렇다는 것은 $i_r$ 의 interval이 $j_r$ 의 interval보다 느리지는 않음을 알 수 있게 합니다. 따라서, 아래 명제는 참이 됩니다.

Theorem 1.

이 greedy algorithm은 optimal solution을 리턴한다.

$Proof.$

당연히 최대 개수를 리턴한다는 사실을 보여야 하는 것입니다. 최대 개수가 아닐 수 있는 상황은 뒤에 한 스케줄을 더 소화할 수 있다는 의미입니다. 그러므로 그런 스케줄이 없다는 것을 보이면 됩니다. 무언가 없다는 것을 보이고 싶을 때는 귀류법을 사용하는 것이 편리할 때가 많습니다.¹ 귀류법을 사용해보겠습니다. 만약, 우리 알고리즘은 $k$개라고 리턴했는데, optimal은 $k+1$ 개라고 가정해보겠습니다. 우리가 앞선 lemma.1에서 보였듯이, 만약 $j_{k+1}$의 interval이 뒤에 $R$에 남아있었다면 그것은 반드시 우리의 $i_k$ interval과 compatible할 것입니다. 우리의 greedy algorithm은 더이상 $R$에 아무것도 남아있지 않을 때까지 실행됩니다. $R$에 무언가 남아있었음에도 불구하고 알고리즘이 종료되었다는 것은 모순입니다. 그러므로 $k$가 optimal한 개수가 맞습니다.

Running time

자연스럽게 우리 알고리즘은 $O(nlogn)$이 걸립니다. 왜냐하면 우리가 사용하는 기준은 가장 빨리 끝나는 interval들부터 소화하기 때문입니다. 이는 바꿔 말하면, $f(b), f(e), f(c), f(h), f(z), …, f(m)$ 등을 빨리 끝나는 순으로 정렬한 후에 앞에서 차례대로 소화하고, 선택된 애와 incompatible한 애들은 지우고(지워도 순서는 유지됩니다), 남은 애들 중에서 또 가장 앞에 있는 애를 선택하는 과정입니다. 그러므로 처음에 정렬할 때 $O(nlogn)$이 걸리고 그 후 과정은 $O(n)$ 걸립니다. 따라서, 전체 시간복잡도는 $O(nlogn)$ 입니다.

정리

앞선 증명 과정의 큰 맥락을 정리해보겠습니다. 우리는 우리의 알고리즘이 사용하는 ‘기준’의 관점(가장 빨리 끝나는 interval을 고르는)에서 볼 때, optimal solution보다 뒤처지지 않는다는 사실을 보인 것입니다. 그 기준은 다양할 수 있습니다. 우리의 greedy algorithm에서 쓰는 기준을 optimal solution $O$에도 적용을 시켜보는 것입니다. 그랬을 때 “그 기준 아래에서 우리의 solution이 optimal solution보다 나쁘지는 않더라(여기서는 우리가 optimal보다 적어도 느린 interval들은 고르지 않더라)”를 보이는 방식입니다. 이것이 바로 stays ahead가 나타내는 바입니다.

• [Stays ahead] 우리가 정한 기준의 관점에서 볼 때 우리의 알고리즘에서 나온 결과 $A$가 다른 어떤 solution $O$보다 그 기준에서는 좋다 또는 unique 하다 : 귀납법 사용
• 이 기준을 따르면 optimal 하다 : 귀류법 사용
  

덧

Scheduling이나 무언가 greedy하게 문제를 풀어야 하는 상황에서는 우선 finishing time을 기준으로 봐주는 것부터 시도해보면 좋습니다.

다음 시간에는 Interval scheduling problem을 Certificate 방식의 증명으로 풀어보겠습니다.

• Algorithm Analysis - Greedy Algorithm 1 ✓ SERIES 1/3
• Algorithm Analysis - Greedy Algorithm 2 SERIES 2/3
• Algorithm Analysis - Greedy Algorithm 3 SERIES 3/3

Algorithm Analysis