Algorithm Analysis: Dynamic Programming 4
알고리즘 관련 모든 글은 연세대학교 안형찬 교수님의 CSI_3108: Algorithm Analysis의 강의 내용과 자료입니다.
이번에는 graph를 다루는 dynamic programming을 정리해보겠습니다. 그전에 앞서 shortest path를 구하는 몇 가지 알고리즘을 짚고 넘어가겠습니다.
- Shortest path problem
- Dijkstra algorithm
- Floyd-Warshall algorithm
- Bellman-Ford algorithm
참고로 또 익히 들어봤을 법한 알고리즘인 Kruskal이나 Prim이 풀어내는 Minimum Spanning Tree(MST) 문제는 여기서의 shortest path와는 다른 문제입니다.
Shortest path problem

이 문제는 우리가 흔히 아는 Dijkstra 알고리즘을 이용해 풀지 못 합니다1. 왜냐하면 여기서는 arc cost2가 양수가 아닐 수 있기 때문입니다. 그렇지만 또다른 가정은 “단, negative cycle은 존재하지 않는다” 입니다. 이런 가정이 없다면 우리는 그 negative cycle을 매우 많이 돌아서 우리의 minimum cost를 계속 낮출 수 있습니다. 결국 우리의 minimum cost값은 그 해당 negative cycle을 몇 바퀴 도는지에 따라 결정됩니다. 무슨 말인지 그림을 보면서 설명하겠습니다.
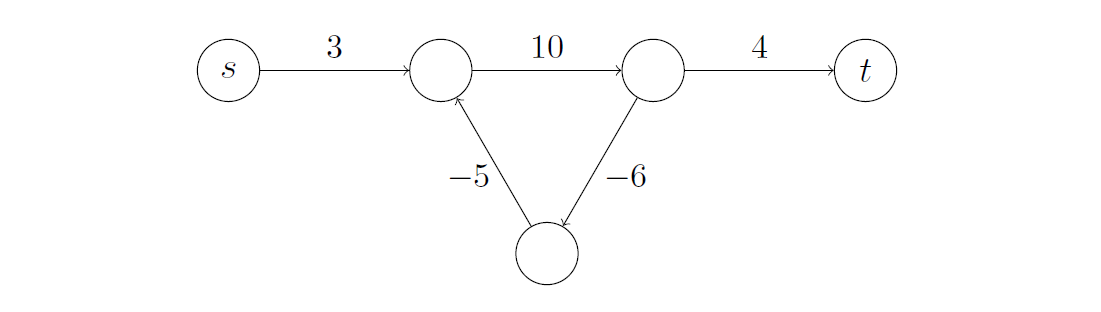
우리가 $s$부터 $t$까지 가는 minimum cost를 찾고 싶다고 가정하겠습니다. 그런데 가운데에 있는 negative cycle을 한 바퀴 돌 때마다 우리는 -1의 cost를 얻게 됩니다. 두 바퀴 돌면 -2, 세 바퀴 돌면 -3 , … 이런 식으로 100바퀴 돌고 $t$에 도달하게 되면 우리는 $3 + (-99) + 4 = -92$ 짜리 shortest path를 얻습니다. 저기서 한 바퀴 더 돌면 $-93$짜리 shortest path를 얻는 셈입니다. 따라서 여기서는 negative cycle은 없다고 가정하겠습니다.
Dijkstra 알고리즘으로 풀지 못 하는 이유
Arc cost가 음수일 때 Dijkstra로 풀지 못 하는 이유는 아래 그림과 같은 이유 때문입니다.
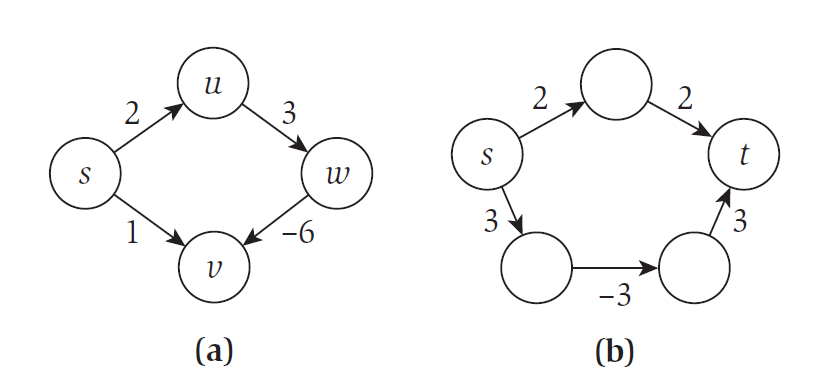
우선 s에서 v로 가는 shortest path를 찾아야 하는 (a)의 경우를 살펴보면 Dijkstra에 의하면 $s-v$의 arc 1개만 가는 것이 가장 shortest라고 할 것입니다. 왜냐하면 그보다 더 많은 edge를 가봤자 edge들의 cost는 모두 양수이기 때문에 edge개수가 가장 적은 게 shortest이기 때문입니다. 하지만 여기서는 이런 접근이 틀립니다. 왜냐하면 사실 저기 돌아돌아 가면 꽤 큰 음수값 arc가 등장하여 여태까지 지나왔던 양수 arc cost를 상쇄시키는 경우가 존재하기 때문입니다.
만약 그렇다면 우리가 충분히 큰 어떤 $X$값을 더해서 모든 cost를 양수로 만들면 Dijkstra로 풀 수 있지 않을까하는 생각이 듭니다. 하지만 이렇게 될 경우에는 minimum cost path가 바뀌게 됩니다. 그림(b)에서는 $s\to t$의 2가지 path가 존재합니다. 우리가 각 edge에 $X$을 더해서 shortest path를 구해보면 위의 path는 $4+2X$ cost를 갖고, 아래의 path는 $3+3X$ cost를 갖습니다. 이처럼 edge 개수에 따라 $X$이 더해지는 횟수가 달라져서 optimal solution을 못 찾습니다. 따라서 우리는 이 문제에서 Dijstra가 아닌 새로운 Bellman-Ford algorithm을 이용하여 풀겠습니다.
추가적인 조건
우리는 여태까지 해왔던 것처럼 dynamic programming을 이용하여 문제에 접근하고 싶습니다. 그래서 특정 $i$번째 vertex까지 도착한 optimal solution을 이용하여 그보다 큰 $i+1$번째 vertex까지의 optimal solution을 구하고 싶습니다. 하지만 여기서 발생하는 문제는, 각 vertex에 순서가 없다는 것입니다. 이를 위해 우리는 추가적인 조건을 달아주겠습니다. 우리가 자료구조 시간에 배우는 topological sort를 하여 각 vertex는 모두 다른 숫자를 부여하는데, directed edge인 arc는 오직 낮은 숫자의 vertex에서 높은 숫자의 vertex로 가게끔 숫자를 부여합니다. 어떤 것인지 그림을 보겠습니다.
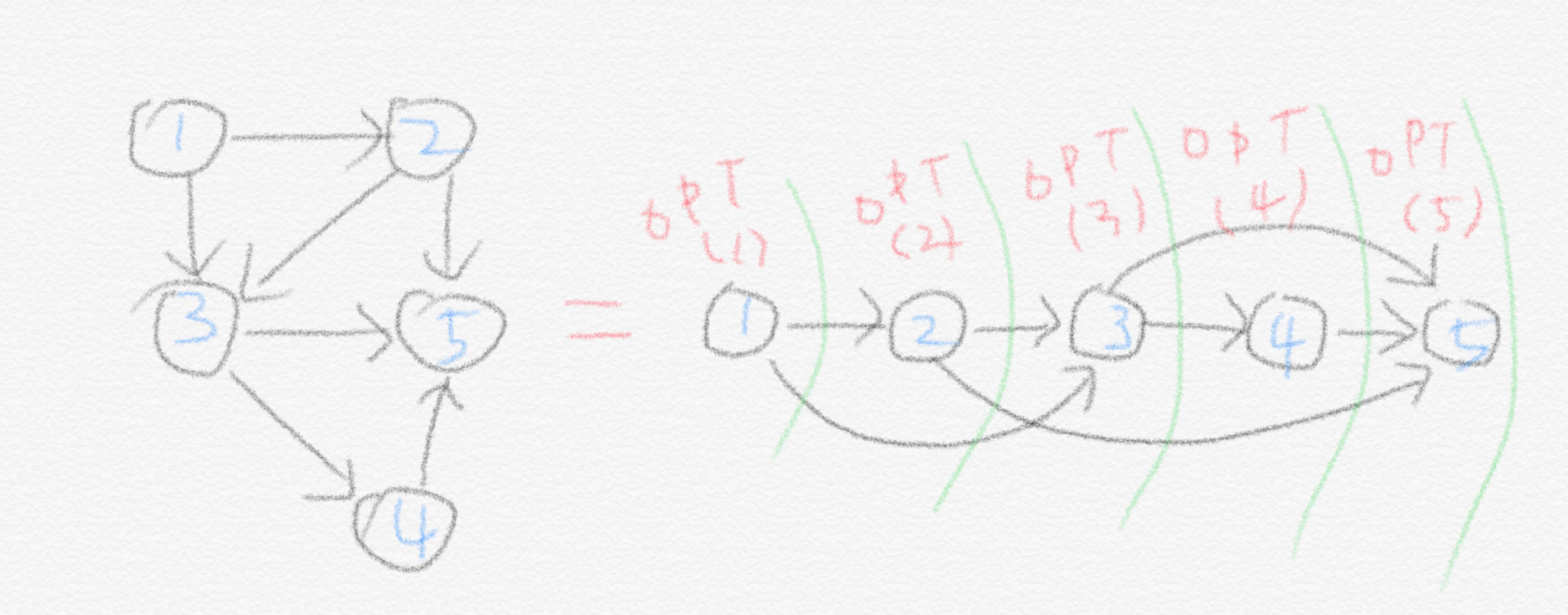
이런 식으로 vertex에 숫자를 부여하면 우리가 지금까지 봐왔던 dynamic programming의 형태로 문제가 재구성되는 것이 보입니다. 그래서 이런 추가적인 조건이 필요했던 것입니다. 이제 우리는 지금까지 해왔던 것처럼 점화식을 세울 수 있습니다.
이 점화식 자체는 참입니다. 하지만 이것만으로는 dynamic programming 방식으로 문제를 풀 수 없습니다. 왜냐하면 우리 가정에서 negative cycle이 존재하지 않는다 하였으므로 positive cycle은 여전히 존재하기 때문입니다. 이 경우 각 vertex사이의 circular reference가 존재할 수 있어서 단순한 $OPT(k)$ 만으로는 풀기 어렵습니다. 그게 왜 문제가 되는지 그림을 통해 좀더 설명하겠습니다.
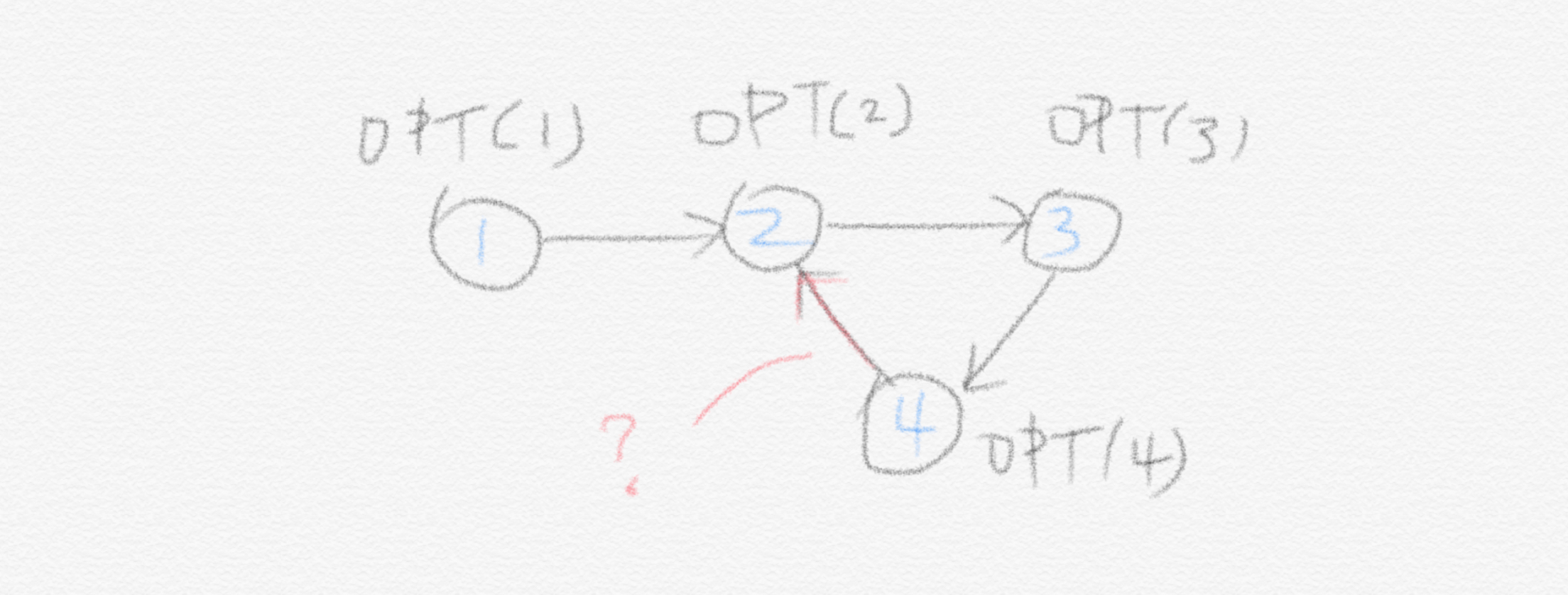
위의 그림을 보면 vertex의 숫자에 따라 $OPT$들이 잘 정의되어 있는 것처럼 보입니다. 하지만 문제가 생깁니다. Dynamic programming에서는 하나의 $OPT()$의 계산에 필요한 다른 $OPT()$들이 미리 계산이 되어 있어야 합니다. 그런데 여기서는 $OPT(2)$는 $OPT(1)$과 $OPT(4)$를 참조하고 있습니다. $OPT(1)$은 이미 계산되어 있겠지만, $OPT(4)$는 계산되어 있지 않습니다. 이렇게 계산되지 않은 $OPT()$를 참조하는 경우가 있기 때문에 위의 점화식으로 당장 dynamic programming을 이용할 수 없는 것입니다.
그렇다면 어떻게 해야 할까요? 사실 생각해보면 $OPT(4)$까지 가려면 edge의 개수가 최소 3개는 필요합니다. 그런데 $OPT(2)$로 가는 데에는 edge 1개면 됩니다. edge 1개면 가는 곳이 어떻게 $OPT(4)$를 참조할까요? Cycle을 $n$번 돈 후에 도달하는 $OPT(2)$는 $OPT(4)$를 참조하게 됩니다. Cycle을 돈다는 사실은 우리가 지나는 edge의 개수가 변한다는 것을 알려줍니다. Edge 3개를 거쳐서 도달한 $OPT(4)$를 $OPT(2)$가 참조합니다. 이때의 $OPT(2)$는 당연히 edge 4개를 거쳐 온(cycle을 한 바퀴 돌고 온 상태) $OPT(2)$가 됩니다. 여기서 저희가 dynamic programming 점화식을 짤 때 반영해야 하는 어떤 무언가가 등장합니다. 바로 edge의 개수입니다. 좀더 일반화시켜 말하면 이전 state의 $OPT()$를 참조하는 것입니다. 새로운 점화식으로 이를 표현해보겠습니다.
풀어서 써보면 edge 1개로 vertex(2)에 도달하는 cost는 edge 0개 써서 각 vertex에 도달한 후, 그 vertex에서 vertex(2)에 연결된 arc cost를 더해주는 것입니다. 하지만 방금 말했듯이 directional graph의 arc이므로 양방향성이 아닙니다. 따라서 사실상 저기서 저희가 고려해주어야 하는 부분은 vertex(2)로 들어오는 arc가 있는 vertex들만 고려하면 됩니다.
vertex(2)가 자기 자신으로 가는 cost는 0이므로 또다시 이렇게 쓸 수 있습니다.
왜 자기 자신으로 오는 arc도 없는데 $OPT(0,2)$를 남기냐고 물을 수 있습니다. 하지만 우리가 dynamic programming에서처럼 해당 문제를 정의하고 싶기에 $OPT()$는 최대 $i$개의 edge를 사용해서 vertex $v$에 도달하는 최소 cost이므로, 만약 최소 edge 2개만을 써서 도달하는 값이 최소이고 다른 경우가 없다면 edge 3개만을 써서 도달하는 최솟값도 같을 것입니다. 또, $OPT(0,4)$는 0으로 놓고(edge를 하나도 쓰지 않고 $vertex(4)$에 도달할 수는 없습니다) 풀면 필요한 값이 미리 계산되어 있지 않은 상황인 circular reference가 사라집니다.
이렇게 어떤 최대 edge를 $i$개를 사용하여 도달하는 최소 cost값을 사용하면 이제 graph문제를 dynamic programming으로 풀 준비가 되었습니다. 앞선 사실들을 이용해서 우리는 dynamic programming table(앞서 봐왔던 배열 $M$)에 최대 arc개수를 제한하는 index를 추가시킵니다. 그렇게 다시 한 번 $OPT(i,v)$를 정의해보면, $OPT(i,v)$는 $s$에서 $v$까지 최대 arc 개수 $i$를 써서 갈 때의 minimum cost입니다. 이제 그 $i$에 어떤 bound가 적용될 수 있는지 살펴보겠습니다.
Lemma 1.
만약 G가 negative cycle을 갖지 않는다면, $s$에서 $t$로 가는 arc 최대 $(n-1)$개짜리 simple path가 존재한다.
$Proof.$
Simple path가 존재한다는 의미는 반복되는 vertex가 없다는 뜻입니다. 실제로 그런 vertex가 없는지 확인해보기 위해 귀류법을 쓰겠습니다. 만약 어떤 path $P$는 simple path가 아니고 특정 vertex $u$가 반복되었다고 가정하겠습니다. 그렇다면 그 두 번의 $u$ 사이의 있는 path를 제외시킨 $P’$는 기존의 $P$보다 작거나 같은 cost를 갖게 됩니다. 왜냐하면 negative cycle이 없다고 가정하였기 때문입니다. 게다가 이런 과정은 path에 포함되어 있는 arc의 개수를 감소시키므로, 이를 반복하면 우리는 언제나 $s$에서 $t$로 가는 arc 최대 $(n-1)$개짜리 simple path를 얻게 됩니다. $s$와 $t$는 그보다 더 멀리 떨어질 수는 없습니다. 왜냐하면 점 $n$개를 직선으로 이으면 그 점과 점 사이에 있는 edge의 개수는 최대 $(n-1)$개이기 때문입니다.
Lemma 2.
$Proof.$
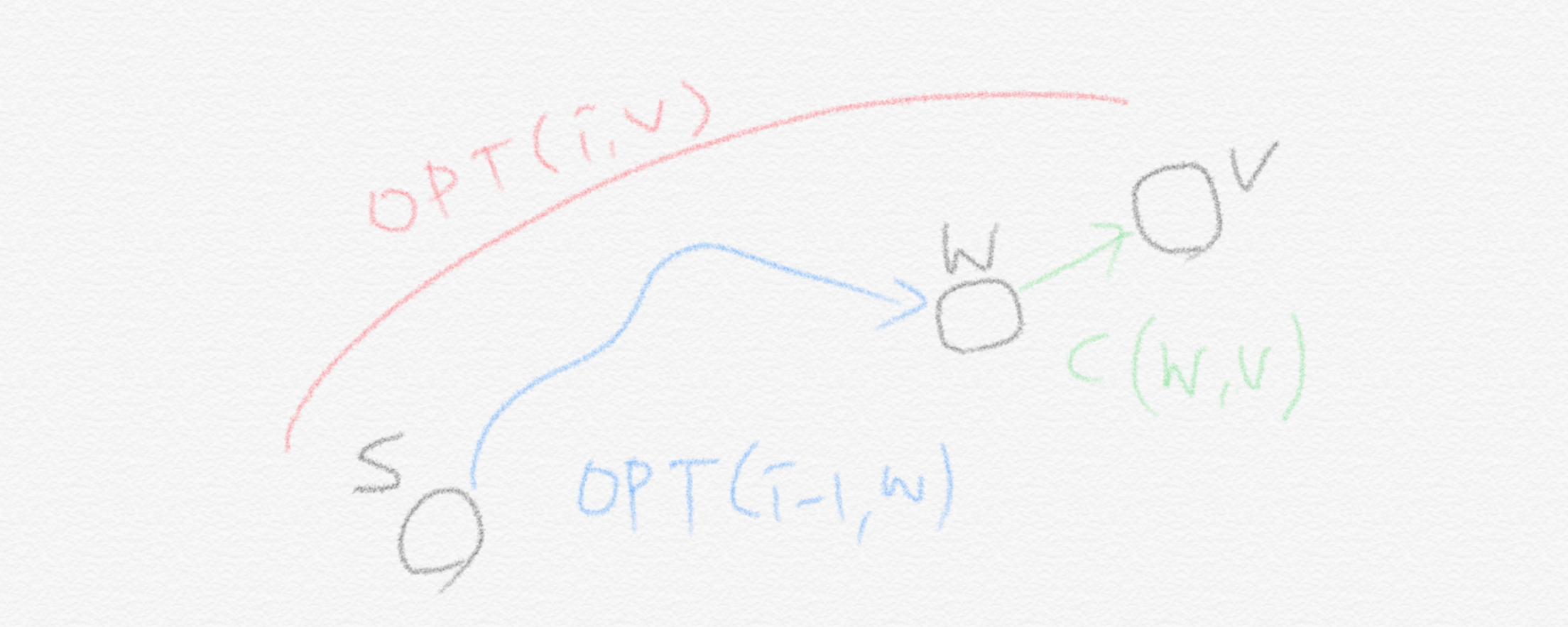
$P$가 만약 최대 $i$개의 arc를 사용해서 $s$에서 $v$까지 가는 path라고 해보겠습니다. 만약 $P$가 $i-1$개만큼의 arc만 쓰고도 $v$에 도달할 수 있으면 $OPT(i,v)=OPT(i-1,v)$이 성립한다. 만약 $(i-1)$개만에 도달할 수 없다면, $<w,v>$가 $P$의 마지막 arc라고 가정해볼 때, 우리가 이를 없앤 $P$는 $s$에서 $w$까지 가는 shortest path가 되므로 $lemma\,\,2$는 성립합니다. 참고를 위해 그림을 첨부합니다.
구현
M[0,s]=0 //s에서 s로는 0개 arc만에 갈 수 있습니다
M[0,s+1~t]=infinity //당연히 0개 arc로 s에서 갈 수 있는 곳은 아무데도 없습니다
for i = 1 to n-1: //최대 n-1 개의 arc
for each w in V: //각 vertex마다 계산합니다
M[i,v]=min(M[i-1,v], min(M[i-1,w]+c(w,v)))
//v에 들어올 수 있는 M들을 다 iterate 해서 min(M[i-1,w]+c(w,v))를 구합니다
return M[n-1,t]
시간복잡도
우선 하나의 $M[i,v]$를 채우기 위해서는 $O(n)$이 걸리고, 그리고 그런 $M$이 $O(n^2)$ 개 있으므로 전체 시간복잡도는 $O(n^3)$입니다. 하지만 잘 생각해보면 시간복잡도는 사실 이보다 작습니다. 정확히 말하면 그래프에 있는 edge의 총 개수를 $m$이라 할 때, 시간복잡도는 $O(n(m+n))$입니다. 설명해보겠습니다.
방금 하나의 $M[i,v]$를 채우기 위해서는 $O(n)$이 걸린다고 하였습니다. 하지만 사실은 그렇지 않습니다. 하나의 $M[i,v]$를 채우기 위해서는 정확히 말하면 $v$로 들어오는 edge만큼만 고려해주면 됩니다. 그런데 여기서는 directed graph를 가정하므로 각 vertex에 들어오는 edge들을 더하면 전체 edge의 개수 $O(m)$이 나옵니다. 또, 전체 vertex를 1번씩 iterate하기 때문에 전체 vertex만큼의 시간 $O(n)$이 걸립니다. 하지만 edge의 개수와 vertex의 개수 중 어떤 것이 더 많고 적은지 모르기 때문에 어느 한 쪽으로 dominate되어서 $O(m)$이나 $O(n)$만 걸리는 상황이 아닙니다. 따라서 안쪽 for문과 점화식 부분은 $DFS$처럼 $O(m+n)$이 걸립니다. 결론적으로 가장 바깥에 있는 for문은 $O(n)$ 시간이 걸리고, 종합해보면 전체 시간복잡도는 $O(n(m+n))$입니다.
정리
그래프 문제를 dynamic programming으로 풀 때는 단순히 vertex의 index만으로 점화식을 짜기 매우 어렵습니다. 왜냐하면 circular reference가 존재할 수 있기 때문입니다. 앞선 dynamic programming 문제들에서 추가 index를 쓰지 않아도 되었던 이유는 circular reference가 존재하지 않았기 때문입니다. 이렇게 dynamic programming에서 추가적인 제약이 필요한 경우에는 index를 추가함으로써 문제를 해결할 수 있습니다. 심지어 어떤 문제는 index를 3개 받아서 $O(n^4)$의 시간복잡도가 나오기도 합니다. 따라서 index를 추가하는 것 자체가 나쁜 일은 아닙니다. Dynamic programming은 자칫 exponential time이 걸릴 수 있는 문제를 memoization 등 여러 방법으로 polynomial time으로 해결하는 것을 미덕으로 생각하는 접근 방식입니다.
덧
Bellman-Ford는 negative cycle이 없다고 가정하고 문제에 접근합니다. 하지만 예를 들어 우리가 negative cycle의 존재 여부를 모르는 상황일 때는 어떻게 하면 될까요? Negative cycle이 있는지를 판별하면 됩니다. 우리가 1번 iteration을 돌고 계산을 마친 후에 또 한 번 돌려봤을 때 또다시 최솟값이 떨어지고, 더 돌릴 때마다 최솟값이 떨어지는 경우라면 negative cycle이 존재한다고 할 수 있습니다.
이상으로 Dynamic programming에 대한 논의를 끝냅니다.
- Algorithm Analysis - Dynamic Programming 1 SERIES 1/4
- Algorithm Analysis - Dynamic Programming 2 SERIES 2/4
- Algorithm Analysis - Dynamic Programming 3 SERIES 3/4
- Algorithm Analysis - Dynamic Programming 4 ✓ SERIES 4/4