read

Algorithm Analysis: Dynamic Programming1

알고리즘 관련 모든 글은 연세대학교 안형찬 교수님의 CSI_3108: Algorithm Analysis의 강의 내용과 자료입니다.

키워드: Decoupling, Memoization

이번 글부터는 dynamic programming을 살펴보도록 하겠습니다. 아래의 문제를 보겠습니다.

Minimum cost travel

Given a sequence of $n+1$ cities $c_0, … , c_n$ and the distance $d_i$ between each consecutive pair of cities ( $c_{i-1}$, $c_i$), determine the minimum cost set of cities to sleep in, subject to the maximum-travel-distance -per-day constraint of $D$. Sleeping in $c_i$ incurs the cost of $p_i$, which is also given as part of the input. The given cities must be traveled exactly in the given order, and we assume that we always pay $p_n$.

city

1차 시도

처음에 우리가 가장 쉽게 이끌어낼 수 있는 방법은 가능한 모든 경우의 수를 돌려보는 겁니다. $c_0$에서 갈 수 있는 도시들을 다 iterate해서 올려보내고, 그리고는 아래 step으로부터 받은 거에 지금 step에서 내릴 decision의 경우의 수를 하나씩 붙여서 가능한 모든 potential을 만들어서 다시 그 위 step으로 올려보냅니다. 이를 pseudocode로 짜보면 이렇습니다.

find AllSchedule(k)
	if k==0:
		return singleton of empty schedule (공집합)
	prevStep_potentials = AllSchedule(k-1)
	thisStep_potentials = {}

	for each schdl in prevStep_potentials:
		append "sleep in city_k" to schdl and add it to thisStep_potentials
		append "don't sleep in city_k" to schdl and add it to thisStep_potentials

	return thisStep_potentials

---------------------------------------
S = AllSchedule(k)
find from S a minimal-cost solution that does not violate the maximum travel distance D.
return the found solution

대략적으로 설명을 해보자면, k번째 도시에서 하나씩 전 단계를 호출하면서 이전 step에서 받은 모든 potential solution들에 지금 step에서 내릴 수 있는 결정(지금 이 k번째 도시에서 잘 것인가, 말 것인가)을 하나씩 붙여서 다시 thisStep_potentials에 넣습니다. 그리고는 그 위 step으로 return해줍니다. 예를 들어보면, OPT(2)에서 리턴되는 thisStep_potentials는 이렇습니다.

$\left\{ (도시1에서잔다, 도시2에서잔다), (도시1에서 잔다,도시2에서 안잔다),\\ (도시1에서안잔다,도시2에서잔다),(도시1에서안잔다, 도시2에서안잔다) \right\}$

결과적으로 우리는 재귀를 선형적으로 호출합니다( $(k+1)$번, AllSchedule(k), AllSchedule(k-1), … ,AllSchedule(0) ). 그럼에도 불구하고 이 알고리즘은 굉장히 비효율적입니다. 이유는 간단합니다. 왜냐하면 우리는 지금 가능한 모든 schedule을 전부 만들었기 때문입니다. 단순히 계산을 해보면 각 step에서는 $2^k$ 번 for문을 돌게 됩니다. 왜냐하면 그 이전 step의 해결책에서 2배씩(이전 step에서 온 것에 잘 건지, 말 건지를 붙인다) 늘어나기 때문입니다.

물론 이렇게 될 경우, 우리가 리턴받은 결과 집합에 solution이 반드시 존재한다는 장점은 있습니다. 하지만 지수함수 꼴로 연산량이 늘어나기 때문에 이는 좋지 않은 알고리즘입니다. 그러므로 알고리즘을 좀더 고쳐보겠습니다.

2차 시도

앞선 시도에서 우리가 배울 점은, 각 재귀 step에서 전달하는 정보의 양이 너무 많으면 좋지 않다는 것입니다. 이전 divide and conquer 에서는 하나의 큰 문제를 작은 subproblem들로 나누어서 풀었습니다. 그리고는 거기에서 얻은 subsolution을 이용하여 solution을 만들었습니다. 여기에도 적용해보겠습니다.

우리가 예를 들어 대전 을 기점으로 2개의 subproblem으로 나누어보겠습니다. 그럴 경우 “서울에서 대전”, “대전에서 부산”까지의 subsolution을 얻어서 이어붙이면 되겠습니다. 하지만 여기서 문제가 발생합니다. 이렇게 나눌 경우 “대전”에서 반드시 자는 solution만 찾기 때문입니다. 하지만 우리의 optimal solution에 대전이 들어가라는 보장은 없기 때문에 이는 좋지 않은 방법입니다.

하지만 이를 이용해서 좀더 좋은 알고리즘을 만들 수 있습니다. 만약 누군가 “대전”이 optimal solution에 들어간다고 알려주면 어떨까요? 그러면 위의 방법은 올바른 solution을 냅니다. 여기서 누군가 “알려준다”는 부분은 알고리즘으로는 불가능하므로 그대신 그런 가능성을 지닌 지점에 대한 $enumeration$으로 만들면 좋은 해결 방법이 되는 경우가 많습니다. 예를 들어 반드시 수원에서 자는 경우로 쪼개보고, 반드시 천안에서 자는 경우로 쪼개보고, … 반드시 밀양에서 자는 경우로 쪼개 보는 겁니다. 이를 Pseudocode로 짜보겠습니다.

function BestSchedule(c_0,c_1, ... , c_n)
	sol = infinity

	//c_0에서 c_n까지 하루만에 도달할 수 있다면
	if sum(d_1, d_2, d_3, ... d_n) <= D:
		sol = min(sol,p_n)
		//그렇다는 말은 c_n에서 1번 잘 때 발생하는 cost만 있기 때문에 p_n만 sol과 비교

	//중간지점으로 삼을 수 있는 모든 도시를 enumerate하면서 그 도시를 기준으로 subproblem을 나눠봅니다
	for i, from 1 to n-1:
		// i번째 도시를 기준으로 나눴을 때
		sol_1 = BestSchedule(c_0, ... , c_i) 첫번째 도시부터 i번째 도시까지의 solution
		sol_2 = BestSchedule(c_i, ... , c_n) i번째 도시부터 마지막 도시까지의 solution
		sol = min(sol, sol_1+sol_2)

	return sol

이 알고리즘은 올바른 solution을 도출해냅니다. 왜냐하면 이 알고리즘 또한 가능한 모든 solution들을 비교하기 때문입니다. 그렇기 때문에 이 알고리즘 또한 비효율적입니다. 하지만 하나 좋은 점은 이렇게 나눈 두 subproblem들이 서로 완벽히 독립이라는 점입니다. 이는 decoupling이라 불리며, Dynamic Programming(DP)에서 매우 중요한 개념 중 하나입니다.

이번 2차시도에서 눈여겨 볼 체크포인트입니다.

문제를 두 subproblem으로 나누었습니다. 하지만 두 subproblem으로 나눌 때 발생하는 문제는, 그 나누는 기준점이 반드시 solution에 들어간다는 보증이 있어야 한다는 점입니다. 보증이 없다면 나누는 기준점이 될 수 있는 모든 점을 enumerate 해보자는 전략입니다.
그리고 이 두 subproblem끼리는 서로 독립입니다(decoupling). 서로가 서로에게 아무 관계가 없습니다. 단지 나누는 기준점만 공유하고 있는 두 subproblem입니다.

그렇지만 이 알고리즘이 비효율적입니다. 생각해보면 <”서울에서 천안”, “천안에서 부산”> 이렇게 나눴던 케이스랑 <”서울에서 천안”, “천안에서 대구”, “대구에서 부산”> 이렇게 나뉘어지는 케이스만 봐도 “서울에서 천안”이 반복되어 계산되고 있습니다. 이 부분을 나중에 좀더 고쳐볼 수 있을 것 같습니다.

또, 좀더 나아가서 생각해보면 애초에 하루 안에 갈 수 있는 최대의 거리 $D$가 정해져있으니, 우리의 마지막 도시에 하루만에 도착할 수 있는 거리에 있는 도시들만 고려할 수 있습니다. 이런 점을 우리 3차 시도에 반영해보겠습니다.

3차 시도

function BestSchedule(c_0, c_1, ... , c_n)
	sol = infinity

	//c_0에서 c_n까지 하루만에 도달할 수 있다면
	if sum(d_1, d_2, d_3, ... d_n) <= D:
		sol = min(sol,p_n)
		//그렇다는 말은 c_n에서 1번 잘 때 발생하는 cost만 있기 때문에 p_n만 sol과 비교

	// 마지막 도시보다 앞에 있는 도시들 중에서
	for i, from n-1 to 1 by -1:
		// 마지막 도시에 하루만에 올 수 있는 애를 골라서
		if sum(d_n, d_{n-1}, ... , d_{i+1}) <= D:
			//그 애에게 도착하는 BestSchedule에 마지막도시에서 자는 cost만 추가한 것이랑 sol이랑 비교해서
			//더 작은 걸 sol에 넣습니다
			sol=min(sol, p_n + BestSchedule(c_0, c_1, ... , c_i))

	return sol

잘 보면 c_0에서 c_n까지 하루만에 오는 경우는 아래 for문에 합쳐질 수 있음을 알 수 있습니다. 왜냐하면 if문은 파라미터로 주어진 첫번째 도시에서 마지막 도시까지 하루만에 갈 수 있는지를 판단하는 단계이고, for문은 ““두번째 도시~ 마지막 전 도시” 중에서 하루만에 마지막 도시에 도달할 수 있는 solution을 찾는 단계이기 때문입니다.

게다가 여기서 파라미터로 넘겨지는 애들은 무조건 그 c_0부터 c_i 까지이므로 파라미터는 그냥 index i로 할 수 있습니다. 그래서 다시 알고리즘을 고쳐보면 이렇습니다.

function BestSchedule(k)
	sol = infinity

	if k==0:
		return p_0

	// 마지막 도시보다 앞에 있는 도시들 중에서
	for i, from n-1 to 0 by -1:
		// 마지막 도시에 하루만에 올 수 있는 애를 골라서
		if sum(d_n, d_{n-1}, ... , d_{i+1}) <= D:
			//그 애에게 도착하는 BestSchedule에 마지막도시에서 자는 cost만 추가한 것이랑 sol이랑 비교해서
			//더 작은 걸 sol에 넣습니다
			sol=min(sol, p_k + BestSchedule(i))

	return sol

그냥 단순하게 생각해서 타겟 도시에 하루만에 도달할 수 있는 도시 중에서 가장 cost가 작은 도시x를 구하는 것입니다. 그리고 그 도시x에 이르는 가장 적은 cost를 갖는 도시y를 또 구합니다. 그렇게 하나 하나 되짚어가다 끝에 다다릅니다. 그리고는 그것들을 다 더하면 되는 셈입니다. 그러면 cost가 작은 것끼리 더해져서 가장 minimal한 cost를 갖게 됩니다. 이 알고리즘이 correct하다는 것은 알 수 있지만 이 알고리즘이 효율적인지 여부는 또 다른 문제입니다. 효율적일까요? 그렇지 않습니다.

왜냐하면 중복이 발생하기 때문입니다. 그것도 아주 체계적으로 중복이 발생합니다. 예시로 $BestSchedule(5)$를 보겠습니다.

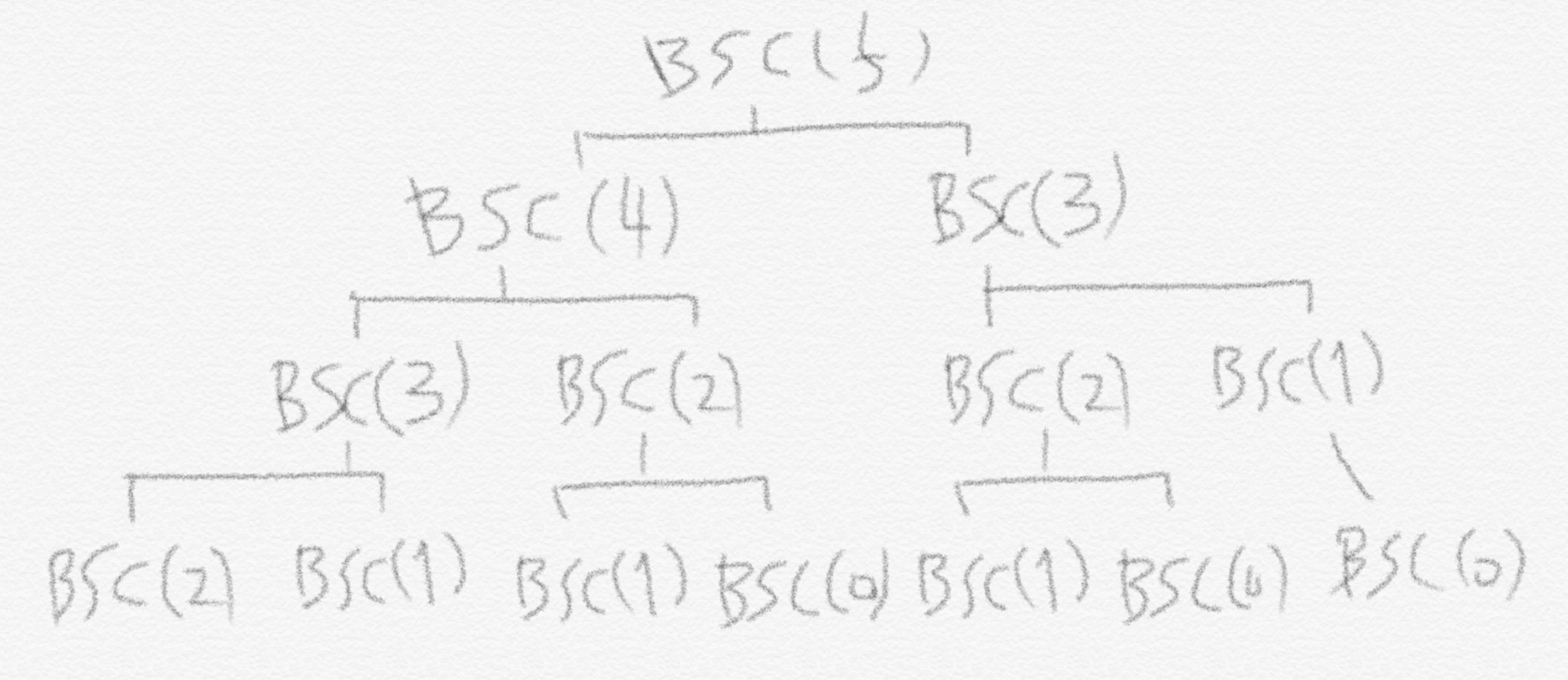
repetition

이를 통해 재귀 호출의 횟수가 최소 피보나치 수열보다는 더 많다는 것을 알 수 있습니다. 예를 들어 $BSC(0)$이 부르는 재귀 호출은 1번(자기 자신 포함)입니다. $BSC(1)$은 자기자신과 $BSC(0)$을 더해서 2번 재귀 호출이 일어납니다. $BSC(2)$는 $BSC(1)$과 $BSC(0)$에 자기 자신을 더하여 2 + 1 + 1 로 4번입니다. 이처럼 어느 도시에 하루만에 도달할 수 있는 도시가 2개씩만 있다고 하더라도 이렇게 비효율적인 알고리즘이 됩니다. 하지만 이를 돌려 생각해보면 $BSC(0), BSC(1), BSC(2), … , BSC(n)$만 미리 다 계산해놓으면 끝나는 문제라는 이야기가 됩니다. 미리 계산해놓고는 각 해당 $BSC(k)$가 필요할 때 바로 불러다 씁니다.

이를 위해 $BSC(0)$에서부터 하나씩 차근차근 쌓아올리면 아직 계산될 수 없는 어떤 $BSC(m)$이 호출되는 일은 존재하지 않습니다. 구현에서는 앞서 계산된 $BSC()$ 결과 값은 행렬 $M$에 하나씩 저장하고 필요할 때 해당 index의 $M$의 원소값을 불러다 쓰는 방법을 사용합니다. 어떻게 보면 계산된 결과값들을 ‘cache’ 해놓는다고 할 수 있겠습니다. 이를 Memoization이라고 합니다. 이를 우리 알고리즘에 녹여보겠습니다.

Memoization

A technique where we “cache” the return values of a recursive function so that we can avoid repeating the same computation.

4차 시도

function BestSchedule(k)
	if k==0:
		return p_0

	// 캐시되어 있는 값이 있다면 그것을 사용합니다
	if M[k] is defined:
		return M[k]

	sol = infinity
	for i from n-1 to 0 by -1:
		if sum(d_n, d_{n-1}, ... , d_{i+1}) <= D:
			sol=min(sol,BestSchedule(i)+p_k)

	//이번 재귀(이번 도시)에서 계산된 cost를 M에 저장해놓습니다(현재 계산되어 있지 않은 상태이니)
	M[k]=sol

	return sol

-----------------------------------------------------
create array M
return BestSchedule(n)

이 알고리즘의 running time에 대해서 이야기해보겠습니다. 이 알고리즘의 주요 부분인 line 9~17은 하나 n값에 대해서 딱 1번씩만 호출이 됩니다. 왜냐하면 앞서 말했듯이 한 번 계산된 결과값은 $M$에 캐시해놓기 때문입니다. 해당 n에 대해 추후 호출되는 $BSC(n)$은 $M[n]$에서 그 결과값을 바로 가져다 씁니다. line 9~17 자체적으로 드는 시간은 $O(n)$입니다. 그리고 $BSC()$에 주어지는 인풋 파라미터도 $O(n)$개입니다($n$개의 도시가 주어집니다). Line 2~7은 어차피 line 12에서 호출되는 $BSC()$ 횟수만큼 실행되므로 $BSC()$ 횟수에 종속됩니다. 따라서 전체적인 시간복잡도는 $O(n^2)$입니다.

정리

Dynamic programming으로 문제를 푸는 큰 틀을 정리해보겠습니다. 우선 우리는 subproblem들에 대한 optimal solution(일단 optimal하다고 가정을 하는 것) 을 이용해 점화식(recurrence relation)을 세웁니다(이런 형태에 대해서는 다음 글부터 더 자세히 다룹니다). 그리고 알고리즘은 점화식을 이용하여 그 subproblem들로부터(decoupling) 더 큰 problem의 optimal solution을 계산해냅니다. 이렇기 때문에 우리는 점화식 내에서 circular reference¹ (subproblem의 solution을 얻기 위해 아직 계산되지 않은 더 큰 problem의 결과를 필요로 하는 경우)가 존재하지 않아야 합니다. Subproblem에 대해 계산된 결과값 subsolution들은 배열에 저장해 놓습니다(Memoization). 그리고는 중복된 연산을 하지 않기 위해 그 배열에 캐시되어 있는 값을 사용합니다. Divide and conquer와 달리 dynamic programming에서는 subproblem들이 대개 더 큰 problem에 비해 조금 더 작은 수준입니다.

왜 조금 더 작아야 하냐면 각 재귀 호출 사이에서 전달되는 정보량이 subsolution table(또는 배열)의 크기를 결정하기 때문입니다. 그리고 이 크기는 알고리즘의 시간복잡도에 영향을 줍니다. 지금은 BSC(i)를 호출하기 때문에 M[i]에서 결과값을 받고 있지만 예를 들어 전달되는 정보가 1개 더 있어서 BSC(i,j) 가 호출되고 있다면 이를 저장하기 위해 2차원 배열이 필요합니다. 그렇기 때문에 시간복잡도가 늘어나게 됩니다.

다음 글에서는 dynamic programming이 적용 가능한 다른 알고리즘들을 살펴보겠습니다.

Algorithm Analysis - Dynamic Programming 1 ✓ SERIES 1/4
Algorithm Analysis - Dynamic Programming 2 SERIES 2/4
Algorithm Analysis - Dynamic Programming 3 SERIES 3/4
Algorithm Analysis - Dynamic Programming 4 SERIES 4/4

circular reference라는 표현을 통해 알 수 있듯이 dynamic programming은 graph로도 표현할 수 있습니다. ↩

Algorithm Analysis

Algorithm Analysis - Dynamic Programming 1 SERIES 1/4