Algorithm Analysis Intro

Blog Logo
on



read

Algorithm Analysis: Intro

알고리즘 관련 모든 글은 연세대학교 안형찬 교수님의 CSI_3108: Algorithm Analysis의 강의 내용과 자료입니다.

Maximum sum of a contiguous subsequence

문제

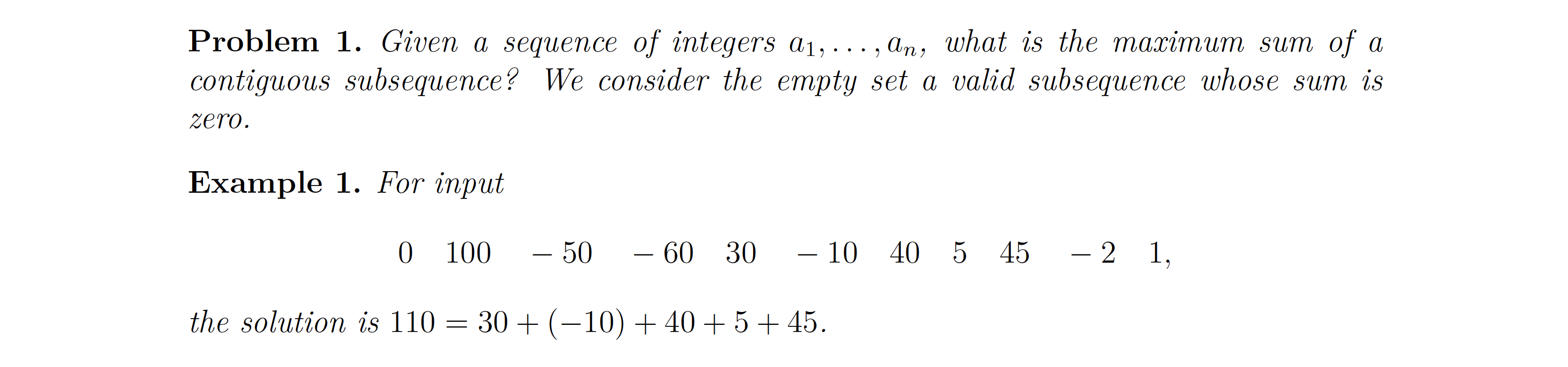
우선 정말 가장 brute force의 방법으로 얼마가 걸리는지 확인해보겠습니다.

1차 시도

sol = 0
//특정 subsequence의 양 끝점입니다 i와 j는.
for i = 1 to n:
	for j = i to n:
		sum = 0
		//그리고 i와 j 사이에 있는 원소들을 하나씩 더해줍니다
		for k = i to j:
			sum = sum + a_k
		if sum > sol
			sol = sum
return sol

이 알고리즘이 기본적으로 하는 일은 무엇이냐면, 시작점 $i$를 하나 잡고, 그 $i$에서 시작하는 모든 subsequence를 계산하는 것입니다. 예를 들면 1번째 원소에서 시작하는 모든 contiguous subsequence의 합을 계산하고 거기서 현재 max값보다 큰 값이 나타나면 max를 없데이트 해줍니다. 1번째 원소 끝났으면 이제 그 다음 2번째 원소에서 시작하는 모든 contiguous subsequence를 계산해주면서 max값을 업데이트합니다. 가능한 모든 contiguous subsequence 중에서 가장 큰 값을 고르는 전형적인 brute force 방법입니다. 시간복잡도는 당연히 $O(n^3)$입니다. 왜냐하면 $i, j, k$ 모두 $n$에 bound되기 때문입니다 ($1\le i \le k \le j \le n $ ).

당연히 이거보다는 더 효율적인 해답이 있을 것입니다. 잘 살펴보면 연산에 굉장히 많은 중복이 이루어지고 있다는 사실을 알 수 있습니다. 예를 들어 $i=3,j=6$일 때와 $i=3,j=7$일 때 $a_3+a_4+a_5+a_6$이 두 경우에서 중복되어 계산되고 있습니다. 분명, 앞선 경우인 $i=3,j=6$에서 $a_3+a_4+a_5+a_6$이 이미 계산되었음에도 불구하고 $i=3,j=7$에서 이 사실을 모르고 또다시 $a_3+a_4+a_5+a_6+a_7$을 처음부터 계산합니다. 알고리즘을 짤 때 좋은 방법 중 하나는 이런 체계적인 중복이 일어나는지 확인하고 이를 제거하는 것입니다. 조금 고쳐서 다시 알고리즘을 짜보겠습니다. 어떻게 하면 좋을까요? 이미 앞선 결과를 어딘가에 저장해놓으면 중복된 연산을 피할 수 있습니다.


2차시도

sol = 0
for i = 1 to n:
	sum_i_i-1 = 0
	for j = i to n:
		//앞선 j에서의 결과를 sum_i_j에 저장해두고 지금 sum_i_j를 계산할 때 불러다 씁니다
		sum_i_j=sum_i_j-1 + a_j
		if sum_i_j> sol
			sol = sum_i_j
return sol

sum[i][j]이라는 2차원 행렬을 만들어 $[i,j]$ 구간에서 계산된 sum값을 저장해둡니다. 그리고는 그 다음 단계($j+1$)에서 그것을 불러서 $a_{j+1}$ 만 더해주고 또다시 이를 sum[i][j+1]에 저장하는 형식입니다. 참고로 말하자면 이는 추후에 dynamic programming에서 볼 memoization과 관계가 있습니다. 아무튼 이렇게 함으로써 이제 시간복잡도가 $O(n^2)$가 되었습니다. 하지만 이보다 더 잘할 수 있을지도 모릅니다.


3차시도

알고리즘의 풀이에서 자주 쓰이는 것 중 하나에 재귀가 있습니다. 마치 mergesort에서 하는 것처럼 문제를 왼쪽과 오른쪽 반으로 쪼개서 그 안에서 각각 maximum subsequence를 찾아보면 어떨까요? 그리고는 두 결과 중에서 더 큰 결과값을 답으로 도출하는 방법입니다. 이 접근방식에는 한 가지 문제가 있습니다. 만약 maximum contiguous subsequence가 왼쪽 subproblem과 오른쪽 subproblem에 걸쳐있는 경우라면 이런 알고리즘은 잘못된 답을 냅니다. 쉽게 말해서 만약 큰 문제를 어떤 기준점을 잡고 양쪽으로 쪼갰는데, 우리가 찾는 해답이 왼쪽 subproblem 어딘가부터 시작해서 오른쪽 subproblem에서 끝나는, 해답이 기준점에 걸쳐있는 경우라면 우리의 알고리즘은 이렇게 실패하게 됩니다.

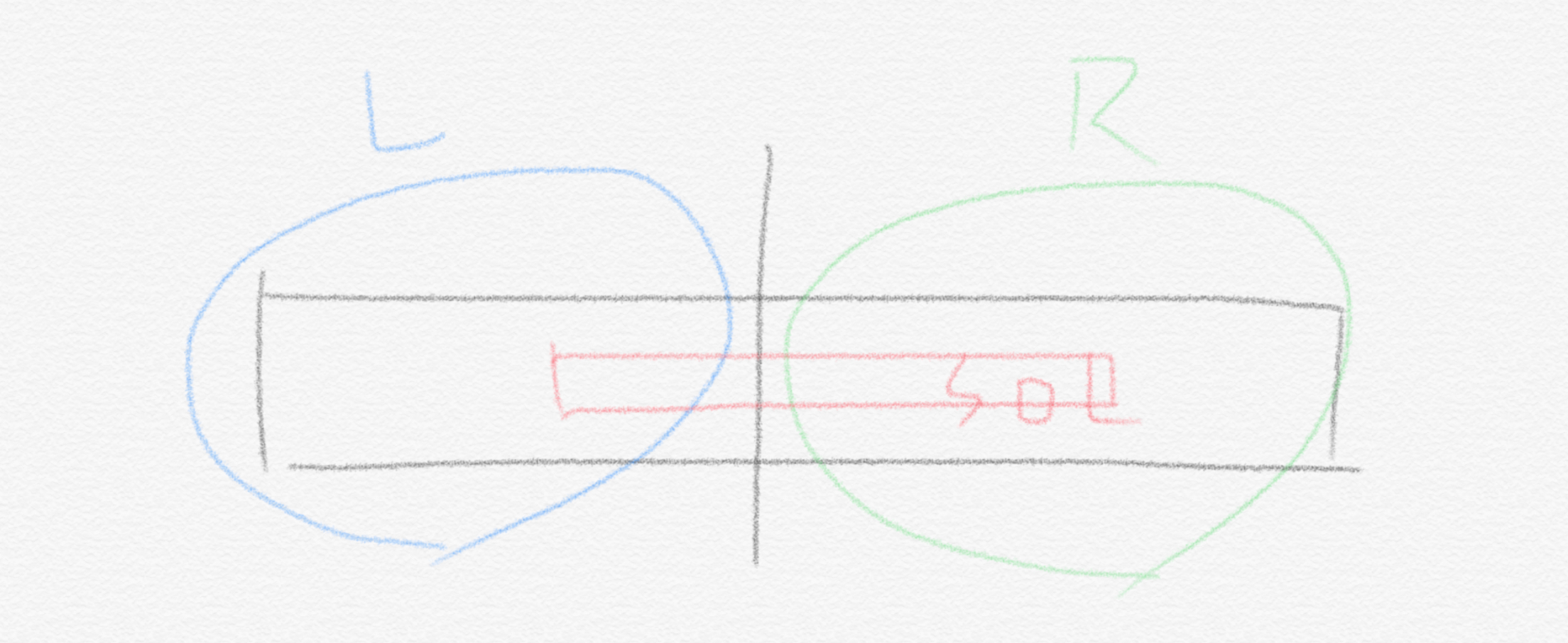
가운데에 걸쳐있는 해답

그래서 어떤 문제를 subproblem으로 쪼갤 때는 그 쪼개는 기준점에 걸쳐있는 solution이 혹시 존재할 수 있는지를 잘 살펴야 합니다. 이를 merging step에서 잘 다뤄야 알고리즘이 문제에 대한 올바른 답을 찾아냅니다. 하지만 이 그림에서 발견할 수 있는 재미있는 점은 바로 저 가운데에 걸쳐있는 solution은 기준점에서 끝나는 subsolution과 기준점에서 시작하는 subsolution의 합이라는 점입니다. 그리고 이런 발견이 우리가 보다 좋은 알고리즘을 만들게 도와줍니다.

function MaxSumSubseq(s,t)
	if s = t
		//왜 0과 비교하냐면 아무것도 없는 sequence도 subsequence로 정의했기 때문입니다
		//만약 모든 값이 음수라면 당연히 아무것도 없는 subsequence가 maximum subsequence가 됩니다
		return max(a_s,0)

	m = (s+t)/2

	//왼쪽 오른쪽 subproblem에서의 solution을 계산합니다
	sol_L = MaxSumSubseq(s,m)
	sol_R = MaxSumSubseq(m+1,t)

	//그리고는 나누는 기준점에서 끝나는 왼쪽 subsolution을 구하고
	subsol_L = 0

	//m에서 시작하여 점점 s(왼쪽)로 갑니다
	//m을 고정으로 시작하여 i까지(최종적으론 s까지)의 subsequence 중 가장 큰 것을 찾습니다
	for i = m,...,s
		if sum(a_i to a_m) > subsol_L:
			subsol_L=sum(a_i to a_m)

	//기준점에서 시작하는 오른쪽 subsolution을 구합니다
	subsol_R = 0

	//여기서는 반대로 m+1에서 시작해서 점점 t(오른쪽)로 갑니다
	//m+1을 고정으로 시작하여 j까지(최종적으론 t까지)의 subsequence 중 가장 큰 것을 찾습니다
	for j = m+1, ..., t
		if sum(a_m+1 to a_j) > subsol_R:
			subsol_R=sum(a_m+1 to a_j)

	//그리고는 3가지 중 더 큰 것을 답으로 취합니다
	return max(sol_L, subsol_L+subsol_R, sol_R)

시간복잡도는 mergesort처럼 $O(n\,logn)$ 입니다. 하지만 이보다 더 잘할 수 있을까요? 만약 누군가 우리에게 올바른 해답이 어떤 특정 기준점을 포함한다는 사실을 알려주었다고 해보겠습니다. 그러면 우리는 그 boundary를 기준으로 당장 merging step을 진행하여 $O(n)$ 에 문제를 풀 수 있습니다. 무슨 말인지 그림을 그려보겠습니다.

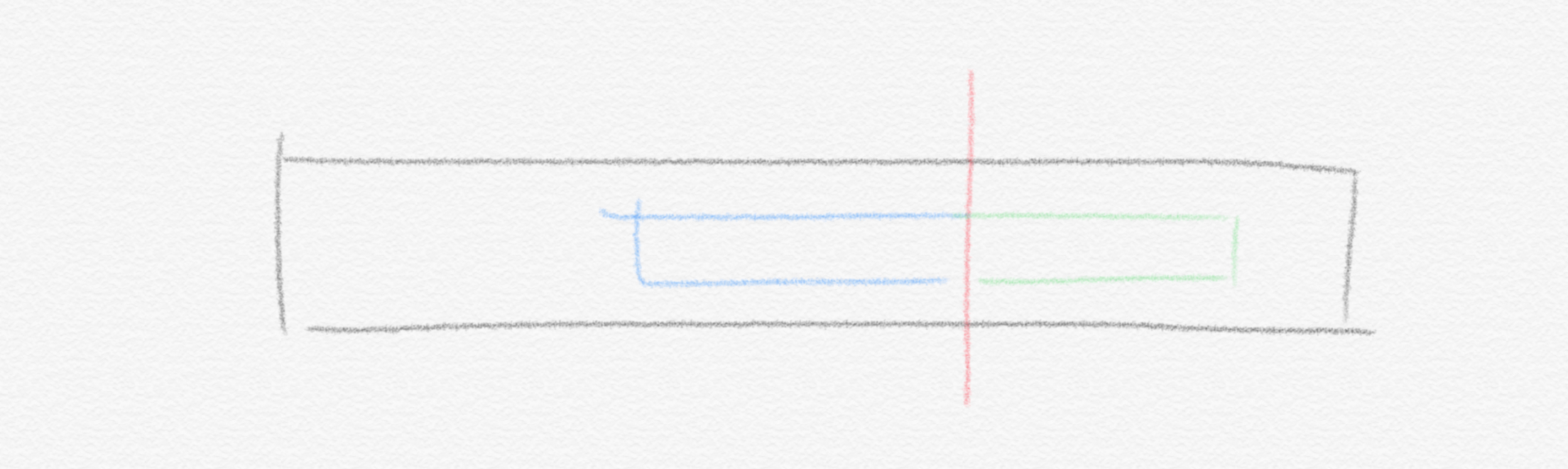
누군가가 알려주기를 저 경계선 위치를 중심으로 해답이 있다고…

누군가 올바른 해답은 저 빨간색 기준점을 포함하고 있다고 알려준다면 우린 그 기준점을 중심으로 위에서 했듯이 subsequence를 찾아나가면 됩니다. 다르게 표현하면, 우리가 바라기를 “해답이 어떤 특정 경계선을 포함하고 있기를 바랄 때, 누군가 그걸 알려주면 좋겠다…” 하고 있을 경우 알고리즘은 이를 위한 다른 접근 방식을 취할 수 있습니다. 그 특정 경계선이 될 수 있는 가능한 모든 지점을 중심으로 iteration을 돌리는 방식입니다. 이해를 돕기 위해 수업 자료의 원문을 그대로 올립니다.

Suppose someone tells us that the optimal solution has to contain the boundary between $a_m$ and $a_{m+1}$ for some $m$. Then, we could immediately perform the merging step of Algorithm 5(여기선 3차시도 알고리즘) and find the optimal solution in $O(n)$ time.

1: wish for $m$ such that a maximum subsequence contains the boundary between $a_m$ and $a_{m+1}$

2: find the maximum subsequence sum that ends at this boundary

3: find the maximum subsequence sum that starts at this boundary

4: return the sum of the two

However, of course, “wishing for an answer” is not an operation that is allowed in an algorithm’s description. We overcome this issue by trying all possible values of $m$

하지만 더 생각해보면 만약 누군가 maximum-sum subsequence가 특정 원소에서 끝이난다고 알려줄 수도 있습니다. 그러면 우리는 그 가능한 끝나는 지점을 중심으로 iteration을 하면 됩니다. 그렇게 알고리즘을 고쳐보겠습니다.


4차시도

MaxEndingAt_1=max(a_1,0)


for m=2, ... , n
	MaxEndingAt_m=max(MaxEndingAt_{m-1}+a_m, 0)
	//왜 0과 MaxEndingAt_{m-1}+a_m 을 비교하냐면, 만약 a_m을 더한 결과가 음수가 되면
	//그 m번째 원소에서 끝나는 최대합 sequence는 차라리 그 음수 sequence보다는
	//empty sequence가 낫기 때문입니다

//그렇게 각 원소에서 끝나는 최대합을 찾았으면 그 최대합 중에서 제일 큰 것을 찾아서 리턴합니다
sol = 0
for m=1, ... , n
	if MaxEndingAt_m > sol
		sol = MaxEndingAt_m

return sol

이렇게 해서 우리는 최종적으로 $O(n)$ 시간복잡도의 알고리즘까지 만들었습니다. 이 알고리즘은 우리가 흔히 말하는 dynamic programming 방법입니다.

정리

여기서 쓰인 여러 전략들은 우리가 앞으로 알고리즘에서 많이 쓰이는 것들입니다. 그래서 정리를 해보겠습니다.

  • 체계적으로 중복되는 연산이 있다면 이를 따로 저장공간을 만들어 cache를 해놓고 불러다 쓰면 시간복잡도가 줄어듭니다
  • 어느 문제를 n가지 subproblem으로 쪼갤 때는 그 subproblem들에 걸쳐 있는 optimal solution이 존재할 수 있습니다
    • 이를 merging step에서 잘 고려해주어야 합니다
    • 또, 이 merging step에서 이미 구했던 다른 subproblem들의 subsolution들보다 좋은 solution이 될 가능성이 있는 애들만 고려해야 합니다. 왜냐하면 merging step에서 너무 많은 시간을 쓰면 안 되기 때문입니다. 예를 들어, subproblem의 값이 5이고, 우리는 최솟값을 찾고 있다면, subproblem 경계에 걸쳐있는 solution의 경우는 5보다 작을 가능성 있는 애들 대상으로 찾아야 합니다.
  • 우리에게 누군가 optimal solution에는 ‘어떤 무언가’가 포함되어 있다고 알려주면 훨씬 문제를 쉽게 풀 수 있는 경우라면 그 ‘어떤 무언가’가 될 가능성이 있는 모든 원소나 경우를 중심으로 iterate 하는 방식으로 문제에 접근할 수 있습니다

Algorithm Analysis

Written by
Blog Logo

순록킴

Published

Supported by