Cross Entropy 파헤쳐보기

• 초보를 위한 정보이론 안내서 - Entropy란 무엇일까 SERIES 1/3
• 초보를 위한 정보이론 안내서 - Cross Entropy 파헤쳐보기 ✓ SERIES 2/3
• 초보를 위한 정보이론 안내서 - KL divergence SERIES 3/3

Entropy에서 Cross entropy까지

이번 글에서는 딥러닝에서 본격적으로 많이 쓰이는 cross entropy 개념에 대해 배워보도록 하겠습니다. 지난 글에서 entropy에 대한 설명을 봤습니다. 그것에 이어서 논의를 진행하겠습니다. 다시 한 번 분포 p의 entropy의 식을 살펴보겠습니다.

지난 번 글에서 봤던 machine 2개를 다시 가져왔습니다. 이번에는 이름을 기계 P와 기계 Q로 하겠습니다.

기계 Q는

• A, B, C, D를 각각 0.25의 확률로 출력

반면, 기계 P는

• A : 0.5
• B: 0.125
• C: 0.125
• D: 0.25

의 확률로 출력합니다.

그리고 지난 글에서 봤듯이 각 기계에 맞는 최적화된 전략은 아래 두 그림에 잘 나타나 있습니다.

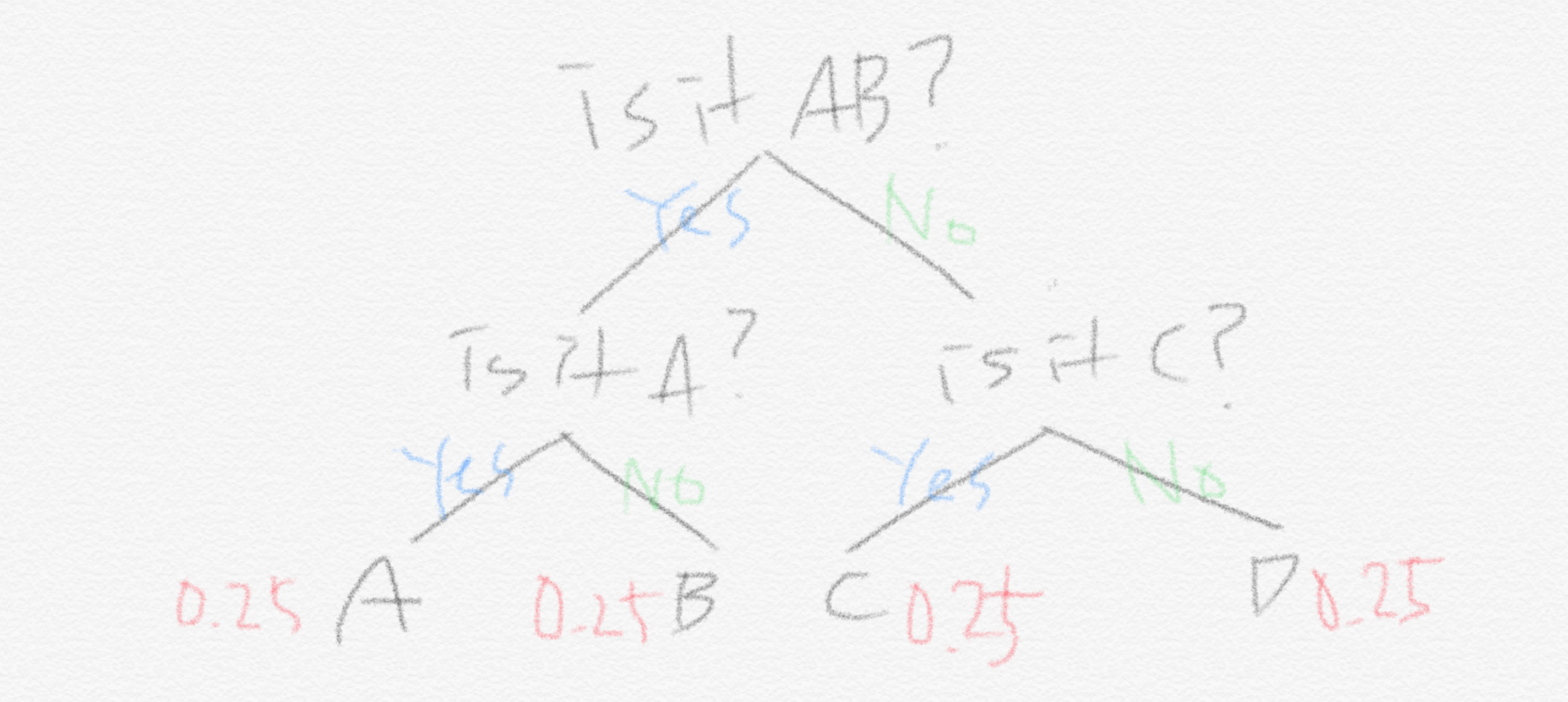
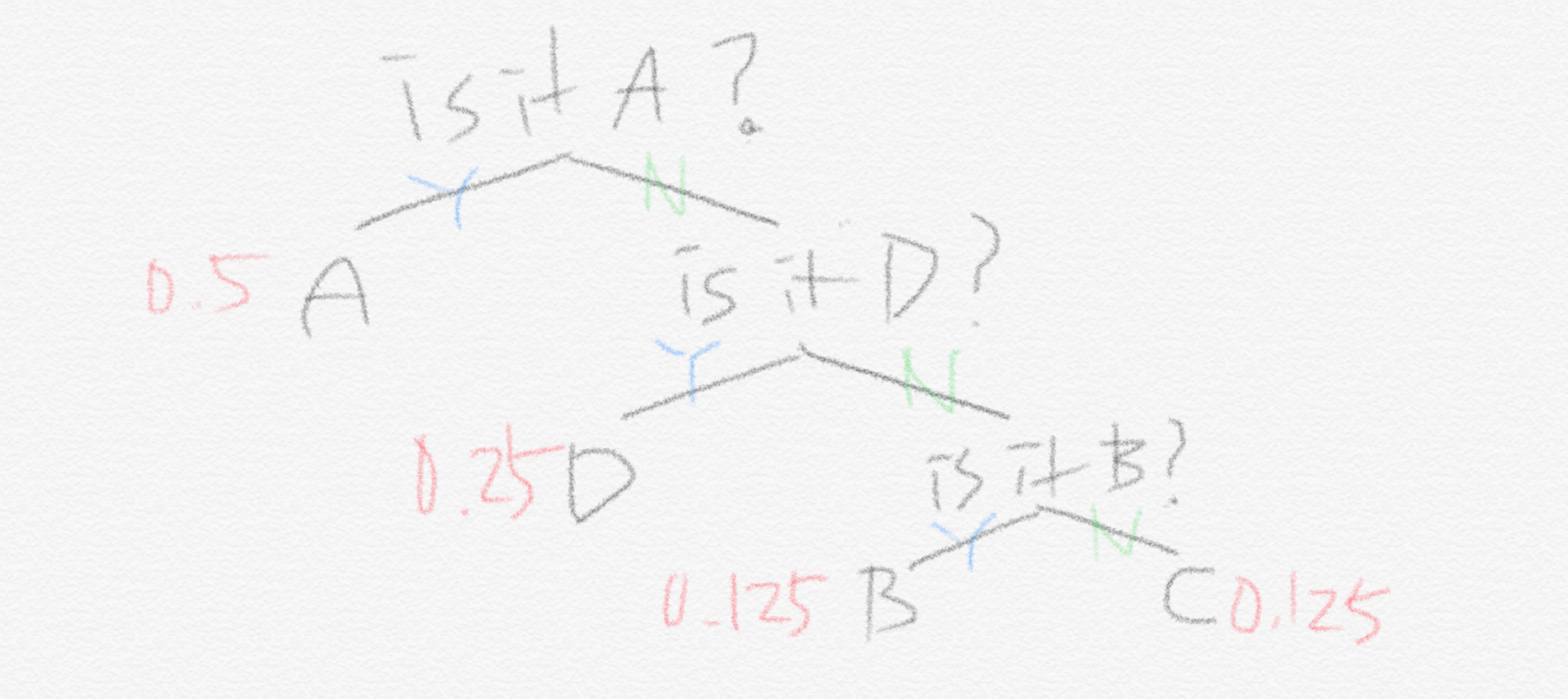
기계 Q에서 entropy 값은 $(0.25 \times 2) \times 4 = 2$ 이고 기계 P에서의 entropy 값은 $0.5 \times 1 +( 0.125 \times 3)\times 2 + 0.25 \times 2 = 1.75$ 입니다. 지난 글에서 말했듯이 확률이 랜덤할수록(다 같은 확률로 등장하는 경우가 가장 랜덤합니다) entropy는 더 높습니다. 결국 entropy라는 것은 최적화된 전략 하에서의 질문개수에 대한 기댓값입니다.

하지만 만약에 다른 전략을 쓴다면 어떻게 될까요? 아래 그림은 우리가 기계 P에 대해서 썼던 전략입니다.

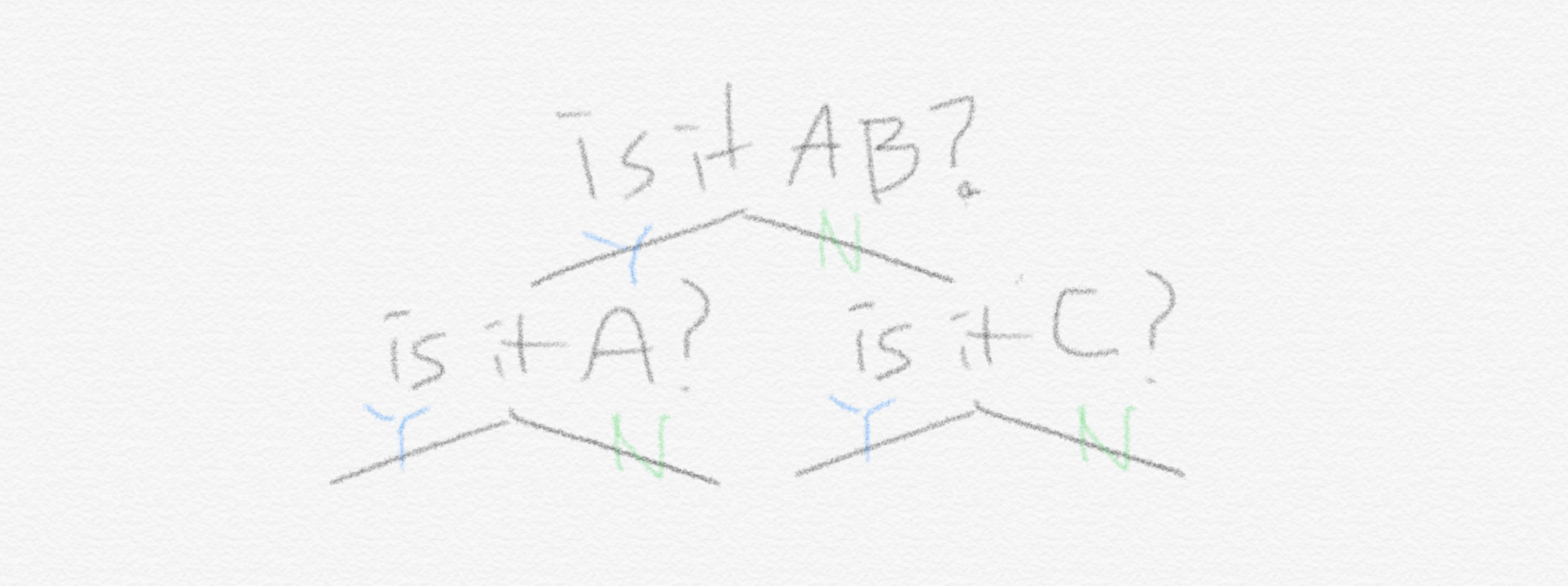
이 전략 Q를 기계 P에 적용해보겠습니다. 그렇다면 앞선 식에서 질문의 개수가 바뀌고 이에 따라 계산된 entropy도 아래처럼 바뀝니다.

기존 $1.75$이던 entropy보다 $0.25$ 더 커진 2가 결과값입니다. 이것이 바로 cross entropy입니다. Cross entropy는 어떤 문제에 대해 특정 전략을 쓸 때 예상되는 질문개수에 대한 기댓값입니다. 여기서 전략 또한 확률분포로 표현된다는 것을 명심해야 합니다. 왜냐하면 전략 Q는 A,B,C,D의 확률이 모두 $0.25$ 라는 가정에서 나오기 때문입니다. 눈치 챘을 수 있지만, 해당 문제(문제도 확률분포로 표현됩니다)에 대한 최적의 전략을 사용할 때 cross entropy 값이 최소가 됩니다. 결국 두 확률분포가 관련된 식입니다. 정리를 해보면 확률분포로 된 어떤 문제 $p$에 대해 확률분포로 된 어떤 전략 $q$를 사용할 때의 질문개수의 기댓값이 바로 cross entropy입니다.

Cross entropy의 다양한 쓰임새

$\begin{align} H(p,q) = & \sum_i p_i \ \log_2{\frac{1}{q_i}} \\ =&-\sum_i p_i \ \log_2{q_i} \end{align}$

Cross entropy를 수식으로 적어보면 이렇습니다. 대개 머신러닝에서 cross entropy를 사용할 때는 이렇습니다: $p_i$가 특정 확률에 대한 참값 또는 목표 확률이고, $q_i$가 우리가 현재 학습한 확률값입니다. 예를 들어 여기서는 $p = [0.5, \ 0.125, \ 0.125, \ 0.25]$ 이고, $q = [0.25, \ 0.25, \ 0.25, \ 0.25]$ 가 되는 셈입니다. 따라서, 우리가 어떤 $q_i$ 를 학습하고 있는 상태라면 $p_i$에 가까워질수록 cross entropy 값은 작아지게 됩니다. 이런 특성 때문에 cross entropy 를 머신러닝에서 많이 쓰는 것입니다. 이산형이 아니라 연속형인 확률분포에서는 시그마가 아니라 integral이 들어오게 됩니다. 따라서 여러분들은 아래의 형태를 자주 보게 될 수도 있습니다.

$-\int p(x) \ \log q(x) dx$

Binary classification과 cross entropy

$-y\log {\hat {y}}-(1-y)\log(1-{\hat{y}})$

우리가 logistic regression에서 보는 cost function입니다. 이 식은 사실 정확하게 cross entropy 식입니다. 하나하나 뜯어보겠습니다. Binary classification에서는 0 또는 1로 두 가지 class를 구분합니다. 이를 수식으로 표현하면 $y \in$ { 0, 1 } 입니다. 우리가 어떤 대상이 1이라고 predict(또는 분류)하는 확률 $q_{y=1}$ 을 $\hat y$ 로 놓겠습니다: $q_{y=1} = \hat y$. 그렇다면 어떤 대상을 0으로 predict하는 확률 $q_{y=0}$ 은 $(1- \hat y)$ 가 됩니다(1 또는 0, 두 가지 결과만 있으므로). 그리고 실제로 어떤 대상이 0 또는 1일 확률(참값) $p_{y=1}, p_{y=0}$ 은 각각 $y$와 $(1-y)$ 가 됩니다. 이제 좀 보이는 것 같습니다. 이 내용을 지금까지 우리가 해왔던 것처럼 정리를 해보면 결국 이런 상황인 것입니다.

$p = \left[\ y, 1-y \ \right] \\ q = \left[ \ \hat{y}, 1-\hat{y} \ \right]$

따라서 logistic regression의 cost function은 단순히 우리가 위에서 봤던 cross entropy의 sigma( $\sum$ )를 풀어쓴 것에 불과했습니다. [Wikipedia 참고]

Cross entropy와 Log loss

[What’s an intuitive way to think of cross entropy? 발췌]

Cross entropy는 log loss로 불리기도 합니다. 왜냐하면 cross entropy를 최소화하는 것은 log likelihood를 최대화하는 것과 같기 때문입니다. 찬찬히 살펴보겠습니다. 어떤 데이터가 0 또는 1로 predict될 확률은 $\hat y$, $1-\hat y$ 이므로 그 데이터의 likelihood 식을 이렇게 세워볼 수 있습니다. ($y$가 0 또는 1의 값만 가질 때 가능합니다)

$\hat{y}^{y} (1-\hat{y})^{(1-y)}$

$y=1$일 때 $\hat y$를 최대화시켜야 하고, $y=0$일 때는 $(1-\hat y)$를 최대화시켜야 합니다. 여기에 $\log$를 씌워보겠습니다. 그러면 지수들이 내려와서 이렇게 됩니다: $maximize \,\, y\log\hat{y} + (1-y)\log(1-\hat{y}) \\ = minimize \,\, -y\log\hat{y} - (1-y)\log(1-\hat{y})$

최소화 해야 하는 식은 우리가 방금 살펴본 cross entropy와 똑같은 식입니다. 이런 이유로 cross entropy를 log loss라고 부르기도 합니다. 왜냐하면 cross entropy 값이 커지면 log likelihood가 작아지기 때문에 cross entropy값을 작게 해야 합니다. 또 나아가 자연스럽게 cross entropy는 negative log likelihood로 불리기도 합니다.

다음 글에서는 cross entropy와 매우 밀접한 연관을 지니며 많이 쓰이는 KL-divergence에 대해 살펴보도록 하겠습니다.

• 초보를 위한 정보이론 안내서 - Entropy란 무엇일까 SERIES 1/3
• 초보를 위한 정보이론 안내서 - Cross Entropy 파헤쳐보기 ✓ SERIES 2/3
• 초보를 위한 정보이론 안내서 - KL divergence SERIES 3/3

Information theory