Information theory
Quantity of information: 정보량
우리는 삶 속에서 늘 ‘이것’을 교환합니다. 인간이라면 누구든 쓰는 언어가 이것의 좋은 매체입니다. 바로 정보입니다. 우리가 질량이나 높이, 속도와 같은 것들을 단위량을 갖고 측정하고 비교하듯이 정보 또한 그럴 수 있습니다. 그때 등장하는 개념이 정보량입니다.
이 정보량의 기원은 어떤 내용을 표현하기 위해 물어야 하는 최소한의 질문 개수에서 출발합니다. 예를 들어 0과 1만 구분하는 전기 신호로 동전을 5번 던진 결과를 전송해야 한다고 가정해보겠습니다. 우리가 물을 수 있는 질문은
“앞면인가요?”
이때 1을 보내면 앞면이고, 0을 보내면 뒷면입니다. 우리는 이 질문을 5번만 하면 됩니다. 만약 10110을 보낸다면, (앞면,뒷면,앞면,앞면,뒷면)이 되겠습니다. 이렇게 1과 0으로 이루어진 5개의 문자열을 보내면 됩니다. 하지만 이보다 복잡하게 알파벳 6개를 보내야 한다고 해보겠습니다. 우리는 어떻게 알파벳 한 글자 한 글자를 1과 0으로 보낼 수 있을까요? 우리가 할 수 있는 최적의 질문전략은, 그 글자가 26개의 알파벳 중에서 앞쪽 절반(A~M)에 속하는지 뒷쪽 절반(N~Z)에 속하는지입니다. 그러면 그때마다 예, 아니오로 대답을 하면 됩니다. 그렇게 최대 5번만 물으면 글자 하나를 추려낼 수 있습니다. 운이 좋으면 4번도 가능합니다. 이를 표현하면 11000 이면 F를 의미합니다. 몇 번 물어야 하는지는 어떻게 알 수 있을까요? 참고로 알파벳은 26개입니다. 절반씩 몇 번을 나누면 되는지, 또는 어느쪽 절반에 속하는지를 몇 번 물어야 하는지를 이렇게 표현할 수 있습니다.
이렇게 될 경우 4.7개의 질문이 한 글자를 추려내기 위해 필요합니다. 그런데 우리는 6글자를 보내야 하니 필요한 질문 개수는 아래와 같습니다.
바꿔 말하면 이렇습니다.
이런 내용을 처음 정립한 것이 R.V.L Hartley입니다. 그는 논문에서 정보를 $H$로 표현합니다.
$n$은 지금 보내는 문자열의 문자(글자, 숫자 등등) 개수, $s$는 각 선택에서 가능한 결과의 가지수입니다(알파벳은 26가지가 가능해서 아까 이었습니다). 한 마디로 말하면 1개의 문자를 구분해내기 위한 질문 개수($log_2{(가능한 \ 결과의 \ 수)}$) 곱하기 몇 개의 문자가 왔는지입니다. 그러면 전체적으로 몇 번의 질문으로 해당 문자열을 파악할 수 있는지가 나옵니다. 가능한 문자열 순서의 가지수가 바로 입니다. 이 정보량을 이렇게 수치화한 것이 정보량입니다. 이제 구체적인 예시를 들며 entropy에 대해 설명해보겠습니다.
Entropy
예를 들어 문자열을 출력하는 2개의 기계 ‘X‘와 ‘Y‘가 있다고 가정해보겠습니다.
기계 X는
- A, B, C, D를 각각 0.25의 확률로 출력
반면, 기계 Y는
- A : 0.5
- B: 0.125
- C: 0.125
- D: 0.25
의 확률로 출력합니다.
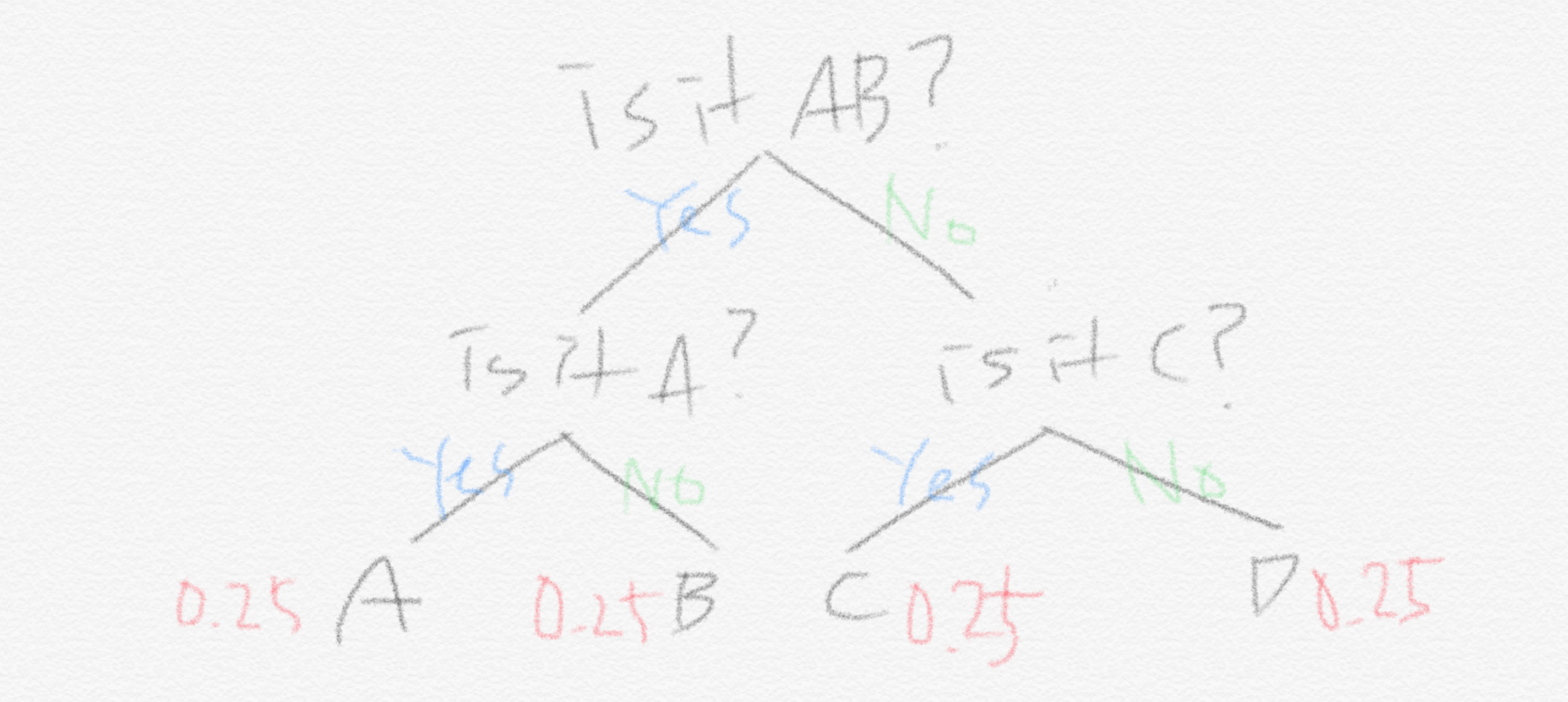
그러면 기계 X가 출력하는 문자 1개를 구분하기 위해서 해야 하는 최소 질문의 개수는 앞서 보인 식에 의하면 2개입니다. 왜냐하면 처음에 (A,B) 중에 있니 (C,D) 중에 있니 라고 반반으로 나눠서 질문하기 때문입니다. 각자 25%씩이니까 A와 B를 합치면 50%입니다. 하지만 기계 Y는 다릅니다.
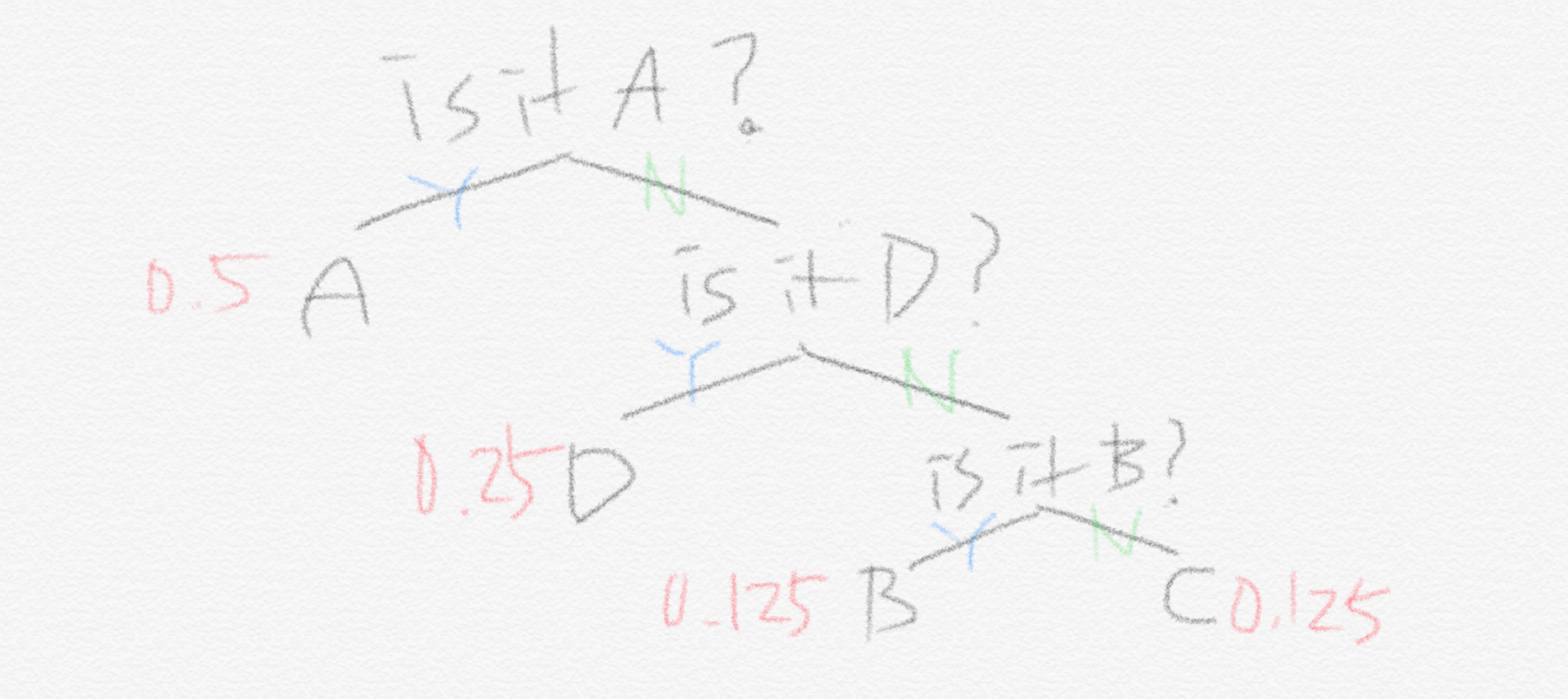
기계 Y의 경우에는 굳이 (A,B)중에 있니 (C,D)중에 있니라고 묻는 전략을 쓰는 것은 비효율적입니다. 왜냐하면 이미 A가 50%의 확률로 나타나기 때문입니다. 그러므로 처음에 물을 때 (A)니 아니면 (B,C,D)중에 있니 라고 묻는 게 옳습니다. 그리고 나서 또 (B,C,D)중에서는 0.5의 확률 중에서 D가 0.25를 차지하고 있으므로 (D)니 아니면 (B,C) 중에 있니 라고 물으면 됩니다. 그렇다면 기계 Y의 경우에 필요한 최소의 질문 개수는 앞서 보였던 단순 로그식으로는 계산이 되지 않습니다. 그 대신 A가 나타날 확률에 A를 추려내기 위한 질문 개수(처음 1개의 질문만으로 A를 추려냅니다)를 곱합니다. 마찬가지로 B가 나타날 확률에 B를 추려내기 위한 질문 개수(3번의 질문으로 추려냅니다)를 곱하고 나머지 C,D에 대해서도 똑같이 하면 됩니다. 이를 식으로 나타내보면 이렇습니다.
그러므로 우리는 1개의 글자를 기계 Y로부터 추려내기 위해서는 평균적으로 1.75개의 질문을 하면 됩니다. 만약 우리가 각 기계가 출력한 100개의 글자를 맞히기 위해서는 기계 X는 200번, 기계 Y는 175번의 질문을 해야 합니다. 그러므로 기계 Y가 X보다 더 적은 정보량을 생산한다고 볼 수 있습니다! 왜냐하면 불확실성(랜덤성)이 더 적기 때문입니다(모든 사건이 같은 확률로 일어나는 것이 가장 불확실합니다). 이를 식으로 정립한 것이 바로 Claude Shannon입니다. Shannon은 이 불확실성의 측정을 ‘Entropy‘라고 불렀습니다. 이를 라고 표시하였고 단위를 bit라고 하였습니다.
생각해보면 질문횟수 A는 1번, B,C는 3번, D는 2번은 A,B,C,D의 발생 확률과 연관이 있습니다.
- A : 0.5 = 1/2
- B: 0.125 = 1/8
- C: 0.125 = 1/8
- D: 0.25 =1/4
그러므로 앞서 말한 ‘가능한 결과의 수’는 그 사건 발생확률의 역수인 셈입니다. 위의 계산 식을 일반화하면 이렇습니다. Shannon이 이야기한 이 식은 이산확률분포일 때의 이야기라는 것을 명심해야 합니다. 이에 따라 시그마가 식에 들어옵니다. 그리고 우리는 일어날 수 있는 각 사건에 대해 값을 구하고 다 더합니다.
Entropy는 가능한 모든 사건이 같은 확률로 일어날 때 그 최댓값을 갖습니다. 그 각각의 확률이 모두 동등한 상황에서 조금만 벗어나도 entropy는 감소합니다. 아래 두 경우를 생각해보겠습니다. $X$의 범위에 걸쳐 특정 값들만 높은 왼쪽 분포가 값들끼리 서로 비슷비슷한 오른쪽 분포보다 entropy가 작습니다.
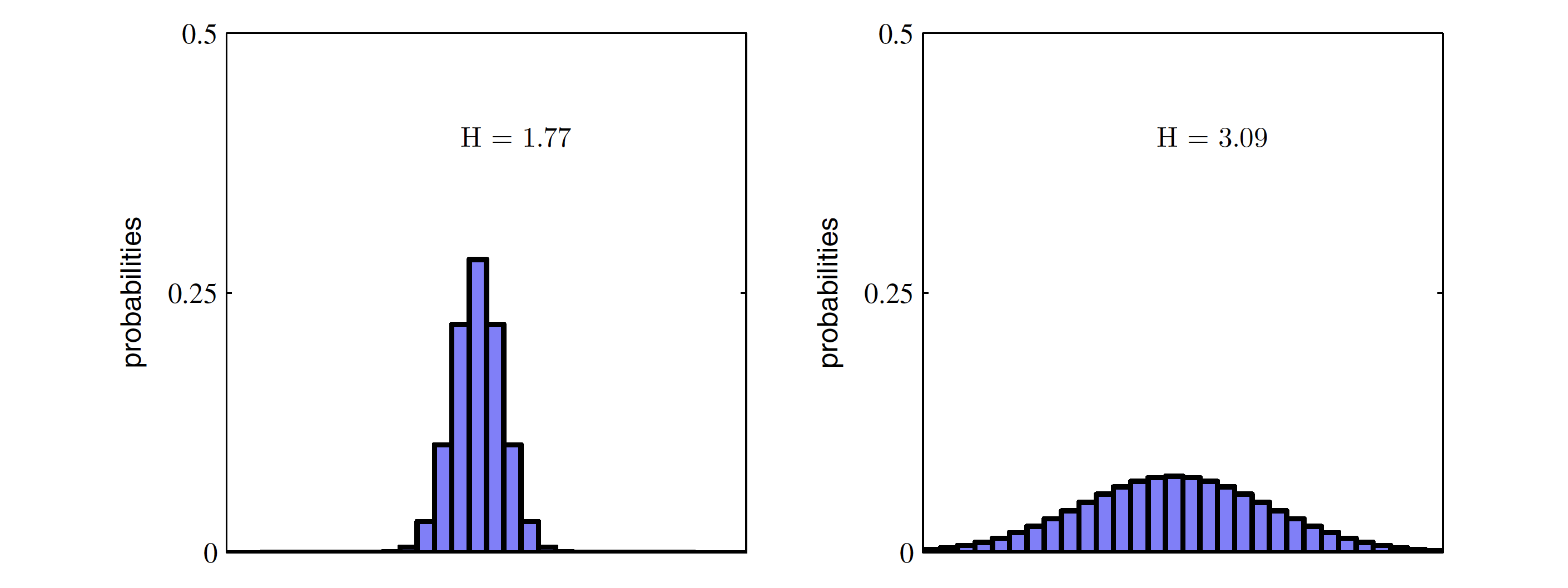
정리하자면, entropy란 최적의 전략 하에서 그 사건을 예측하는 데에 필요한 질문 개수를 의미합니다. 다른 표현으로는 최적의 전략 하에서 필요한 질문개수에 대한 기댓값입니다. 따라서, 이 entropy가 감소한다는 것은 우리가 그 사건을 맞히기 위해서 필요한 질문의 개수가 줄어드는 것을 의미합니다. 질문의 개수가 줄어든다는 사실은 정보량도 줄어든다는 의미입니다.
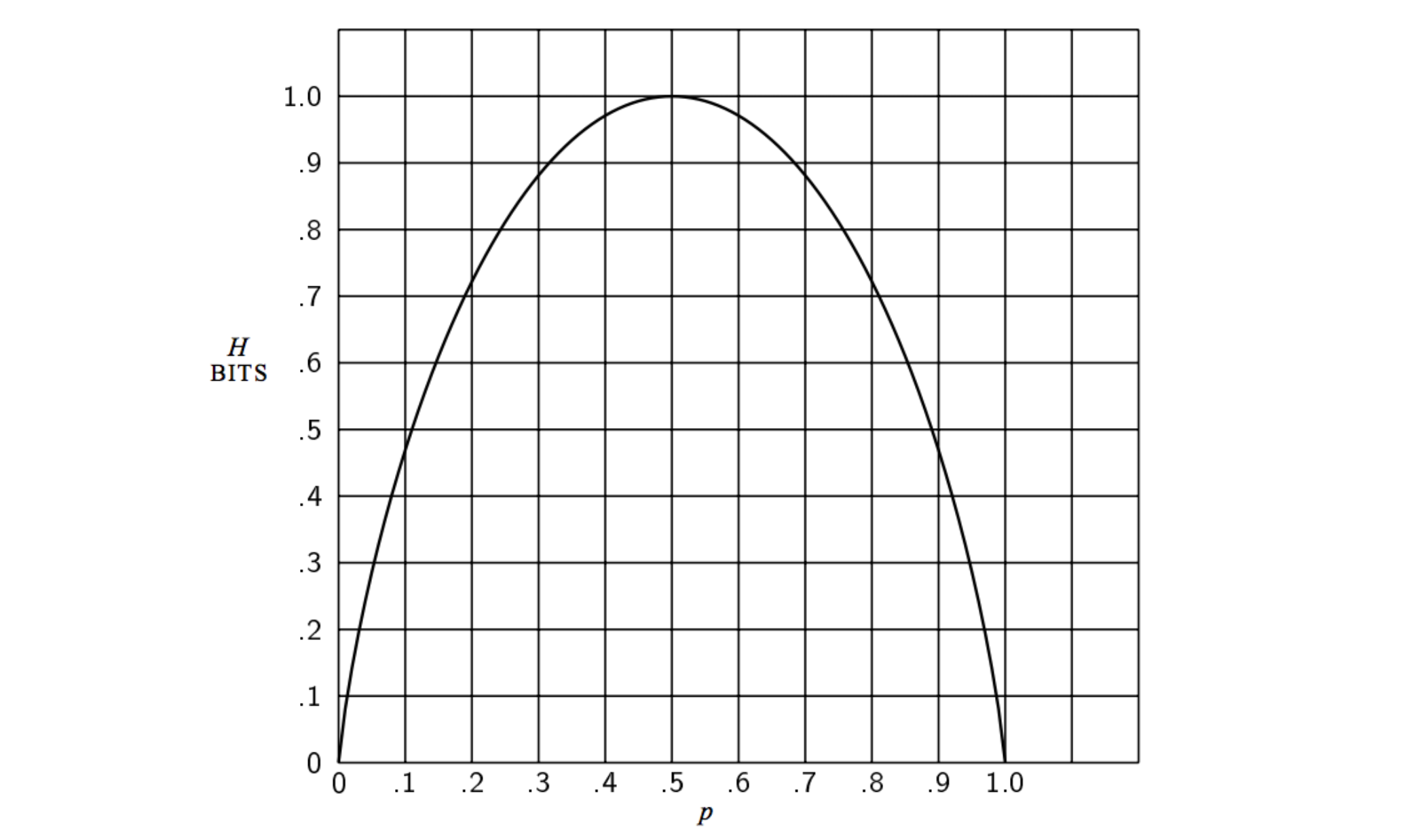
[C.E. Shannon, A Mathematical Theory of Communication, 1948]
- 초보를 위한 정보이론 안내서 - Entropy란 무엇일까 ✓ SERIES 1/3
- 초보를 위한 정보이론 안내서 - Cross Entropy 파헤쳐보기 SERIES 2/3
- 초보를 위한 정보이론 안내서 - KL divergence SERIES 3/3